Evaluation of drag force on a nonuniform particle distribution with a meshless method--颗粒学报PARTICUOLOGY

Wang, X., & You, C. (2011). Evaluation of drag force on a nonuniform particle distribution with a meshless method. Particuology, 9(3), 288–297. https://doi.org/10.1016/j.partic.2010.02.002

Evaluation of drag force on a nonuniform particle distribution with a meshless method

Xi Wang, Changfu You^*

Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Thermal Engineering, Tsinghua University, Beijing 100084, China

10.1016/j.partic.2010.02.002

Volume 9, Issue 3, June 2011, Pages 288-297

Received 13 October 2009, Revised 18 January 2010, Accepted 20 February 2010, Available online 1 April 2011.

E-mail: youcf@tsinghua.edu.cn

Highlights

Abstract

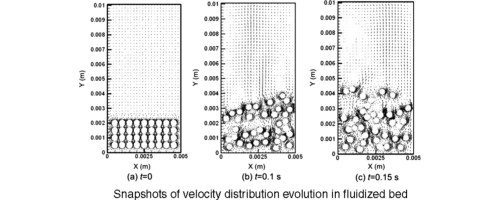
A meshless Element-Free Galerkin (EFG) method was used to directly simulate the fluidization process in two dimensions. The drag force on particles was obtained by integrating the stress and shear forces on the particle surfaces. The results show that meshless methods are capable of dealing with real particle collisions, thus are superior to most mesh-based methods in reflecting the fluidization process with frequent particle collisions and suitable void fractions. Particle distribution greatly influences the drag coefficients even for the same voidage, that is, there are large differences in the average drag coefficients between nonuniform and uniform particle distributions. Different compacting directions also have different regularities, so conventional formulas such as ‘Wen and Yu’ and ‘Felice’ models have some deviations in such nonuniform distributions. To evaluate the influence of the nonuniformity, the drag force in multiple particle systems was simulated by using nonuniformity coefficients, C_VX and C_VY, to quantitatively describe the nonuniform distribution in different directions. Drag force during fluidization can be successfully evaluated by the use of CVX alone.

Graphical abstract

Keywords

Meshless method; Drag force; Nonuniform particle distribution; Nonuniformity coefficient

文章导读