Numerical simulation of sedimentation of rectangular particle in Newtonian fluid--颗粒学报PARTICUOLOGY

Lv, H., Tang, S., & Zhou, W. (2012). Numerical simulation of sedimentation of rectangular particle in Newtonian fluid. Particuology, 10(1), 79–88. https://doi.org/10.1016/j.partic.2011.04.008

Numerical simulation of sedimentation of rectangular particle in Newtonian fluid

Hong Lv, Shengli Tang^*, Wenping Zhou

Department of Power Engineering, Chongqing University, Chongqing 400030, PR China

10.1016/j.partic.2011.04.008

Volume 10, Issue 1, February 2012, Pages 79-88

Received 25 January 2011, Revised 12 April 2011, Accepted 21 April 2011, Available online 8 November 2011.

E-mail: tytsl@cqu.edu.cn

Highlights

Abstract

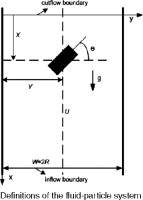
The sedimentation of a rectangular particle falling in a two-dimensional channel filled with Newtonian fluid was simulated with finite element arbitrary Lagrangian–Eulerian domain method. The numerical procedure was validated by comparison of the simulation results with existing numerical work. Moreover, good agreement was obtained between the simulation results and experimental measurements performed in the current study. The equilibrium position, stable orientation and drag coefficient of a rectangular particle for different particle Reynolds numbers (Re_p) were studied. The results show that there is a critical particle Reynolds number for the preferred orientation of a rectangular particle falling in a Newtonian fluid. When Re_p is smaller than the critical value, the particle falls with its long side parallel to gravity; otherwise the particle falls with its long side perpendicular to gravity. The critical particle Reynolds number is a decreasing function of the blockage ratio and aspect ratio. The distributions of pressure and shear stress on rectangular particle surface were analyzed. Moreover, the drag coefficient of the rectangular particle decreases as Re_p or the blockage ratio increases; however, it appears to be independent of aspect ratio.

Graphical abstract

Keywords

Rectangular particle; Drag coefficient; Sedimentation; ALE method; Direct numerical simulation

文章导读