Effect of wall boundary condition on CFD simulation of CFB risers--颗粒学报PARTICUOLOGY

Zhou, X., Gao, J., Xu, C., & Lan, X. (2013). Effect of wall boundary condition on CFD simulation of CFB risers. Particuology, 11(5), 556–565. https://doi.org/10.1016/j.partic.2012.08.006

Effect of wall boundary condition on CFD simulation of CFB risers

Xinyu Zhou, Jinsen Gao, Chunming Xu, Xingying Lan^*

State Key Laboratory of Heavy Oil Processing, China University of Petroleum, Beijing 102249, China

10.1016/j.partic.2012.08.006

Volume 11, Issue 5, October 2013, Pages 556-565

Received 2 December 2011, Revised 4 August 2012, Accepted 14 August 2012, Available online 2 April 2013.

E-mail: lanxy@cup.edu.cn

Highlights

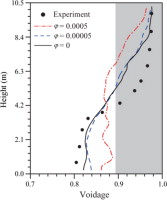
• Hydrodynamics of gas–solid flow in a CFB riser were simulated using two-fluid model.

• Gidaspow- and EMMS-based drag models and different wall boundary conditions were used.

• Effect of wall boundary condition on hydrodynamics of CFB was closely related to drag model used.

• Small specularity resulted in better agreement with experiments while using EMMS-based drag model.

Abstract

The effect of solid-phase wall boundary condition on the numerical simulation of gas–solid flow in CFB risers containing FCC particles was investigated using the two-fluid model incorporating the kinetic theory of granular flow. Both the Gidaspow drag model and the EMMS-based drag model were used. The Johnson and Jackson (1987) wall boundary condition was applied to describe the interaction between particles and wall. Based on the experimental system of Li and Kwauk (1994), parametric studies of specularity coefficient (φ = 1.0, 0.6, 0.0005, 0.00005, 0) and particle–wall restitution coefficient (e_w = 0.6, 0.9, 0.95, 0.99, 0.999) were performed to evaluate their effects on axial voidage profile, solids flux, meso-scale and heterogeneous structures. Simulation results showed that solid-phase wall boundary condition had little effect on axial voidage profile when the Gidaspow drag model was used. However, the specularity coefficient φ had a pronounced influence on flow behavior when the EMMS-based drag model was used, and a small specularity coefficient (φ = 0.00005, 0) could result in better agreement with experimental data. The particle–wall restitution coefficient e_w plays but a minor role in the holistic flow characteristics.

Graphical abstract

Keywords

Circulating fluidized bed; Boundary condition; EMMS; CFD; Specularity coefficient; Particle-wall restitution coefficient

文章导读