Effects of polydispersity on the micro–macro behavior of granular assemblies under different deformation paths--颗粒学报PARTICUOLOGY

Kumar, N., Imole, O. I., Magnanimo, V., & Luding, S. (2014). Effects of polydispersity on the micro–macro behavior of granular assemblies under different deformation paths. Particuology, 12, 64–79. https://doi.org/10.1016/j.partic.2013.07.011

Effects of polydispersity on the micro–macro behavior of granular assemblies under different deformation paths

Nishant Kumar^*, Olukayode I. Imole, Vanessa Magnanimo, Stefan Luding

Multi Scale Mechanics (MSM), Faculty of Engineering Technology, MESA+, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands

10.1016/j.partic.2013.07.011

Volume 12, February 2014, Pages 64-79

Received 25 March 2013, Revised 5 July 2013, Accepted 15 July 2013, Available online 19 November 2013.

E-mail: n.kumar@utwente.nl

Highlights

• We study the effects of polydispersity under isotropic, deviatoric and uniaxial compression paths.

• Isotropic quantities show a systematic dependence on the deformation mode via the jamming volume fraction.

• We present relations for jamming volume fraction as function of polydispersity and deformation mode.

• A simplified constitutive model involving structural anisotropy is presented.

• The predictive capacity of the calibrated model is tested by comparison with an independent test.

Abstract

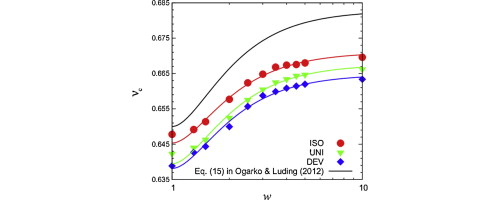
The micromechanical and macromechanical behavior of idealized granular assemblies, made by linearly elastic, frictionless, polydisperse spheres, are studied in a periodic, triaxial box geometry, using the discrete element method. Emphasis is put on the effect of polydispersity under purely isotropic loading and unloading, deviatoric (volume conserving), and uniaxial compression paths.

We show that scaled pressure, coordination number and fraction of rattlers behave in a very similar fashion as functions of volume fraction, irrespective of the deformation path applied. Interestingly, they show a systematic dependence on the deformation mode and polydispersity via the respective jamming volume fraction. This confirms that the concept of a single jamming point has to be rephrased to a range of variable jamming points, dependent on microstructure and history of the sample, making the jamming volume fraction a state-variable.

This behavior is confirmed when a simplified constitutive model involving structural anisotropy is calibrated using the purely isotropic and deviatoric simulations. The basic model parameters are found to depend on the polydispersity of the sample through the different jamming volume fractions. The predictive power of the calibrated model is checked by comparison with an independent test, namely uniaxial compression. The important features of the uniaxial experiment are captured and a qualitative prediction for the evolution of stress and fabric is shown involving a “softening” regime in both stress and fabric – stronger for the latter – that was not prescribed into the model a priori.

Graphical abstract

Keywords

Polydispersity; Anisotropy; Deformations; Calibration; PARDEM

文章导读