A stability condition for turbulence model: From EMMS model to EMMS-based turbulence model--颗粒学报PARTICUOLOGY

Zhang, L., Qiu, X., Wang, L., & Li, J. (2014). A stability condition for turbulence model: From EMMS model to EMMS-based turbulence model. Particuology, 16, 142–154. https://doi.org/10.1016/j.partic.2014.02.003

A stability condition for turbulence model: From EMMS model to EMMS-based turbulence model

Lin Zhang ^a, Xiaoping Qiu ^{a b}, Limin Wang^a *, Jinghai Li ^a

a The EMMS Group, State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China
b University of Chinese Academy of Sciences, Beijing 100049, China

10.1016/j.partic.2014.02.003

Volume 16, October 2014, Pages 142-154

Received 18 November 2013, Revised 31 December 2013, Accepted 26 February 2014, Available online 4 April 2014.

E-mail: lmwang@ipe.ac.cn

Highlights

• An EMMS-based meso-scale turbulence model was proposed.

• The stability condition was successfully applied for the closure of turbulence model.

• Structure of turbulent flow was separated by two-phase concept of turbulence.

• Energy dissipation was quantified with drop/bubble breakup model in turbulent dispersions.

• Accurate simulation of turbulent flows on the coarse grid was achieved.

Abstract

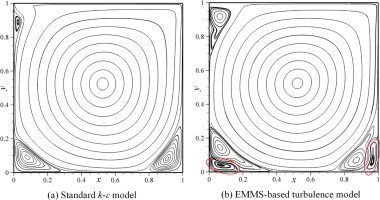
The closure problem of turbulence is still a challenging issue in turbulence modeling. In this work, a stability condition is used to close turbulence. Specifically, we regard single-phase flow as a mixture of turbulent and non-turbulent fluids, separating the structure of turbulence. Subsequently, according to the picture of the turbulent eddy cascade, the energy contained in turbulent flow is decomposed into different parts and then quantified. A turbulence stability condition, similar to the principle of the energy-minimization multi-scale (EMMS) model for gas–solid systems, is formulated to close the dynamic constraint equations of turbulence, allowing the inhomogeneous structural parameters of turbulence to be optimized. We name this model as the “EMMS-based turbulence model”, and use it to construct the corresponding turbulent viscosity coefficient. To validate the EMMS-based turbulence model, it is used to simulate two classical benchmark problems, lid-driven cavity flow and turbulent flow with forced convection in an empty room. The numerical results show that the EMMS-based turbulence model improves the accuracy of turbulence modeling due to it considers the principle of compromise in competition between viscosity and inertia.

Graphical abstract

Keywords

Stability condition; Mathematical modeling; Turbulence; EMMS; Hydrodynamics; Computational fluid dynamics

文章导读