Investigation into improving the efficiency and accuracy of CFD/DEM simulations--颗粒学报PARTICUOLOGY

Alobaid, F., Baraki, N., & Epple, B. (2014). Investigation into improving the efficiency and accuracy of CFD/DEM simulations. Particuology, 16, 41–53. https://doi.org/10.1016/j.partic.2013.11.004

Investigation into improving the efficiency and accuracy of CFD/DEM simulations

Falah Alobaid^*, Nabil Baraki, Bernd Epple

TU Darmstadt, Energiesysteme und Energietechnik, Petersenstrasse 30, 64287 Darmstadt, Germany

10.1016/j.partic.2013.11.004

Volume 16, October 2014, Pages 41-53

Received 7 July 2013, Revised 1 November 2013, Accepted 6 November 2013, Available online 17 January 2014.

E-mail: falah.alobaid@est.tu-darmstadt.de

Highlights

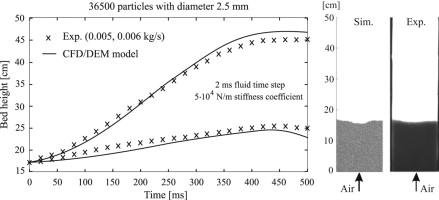
• Fluid time steps between 1 and 5 ms were suggested for a compromise between efficiency and accuracy.

• Stiffness coefficients between 10⁴ and 10⁶ N/m offered a compromise between efficiency and accuracy.

• Parallelized CFD/DEM simulation should not exceed the critical number of domain decomposition.

• Using higher parallelized CPU number made gains in computation time for increased solid loading.

Abstract

The Euler–Lagrange approach combined with a discrete element method has frequently been applied to elucidate the hydrodynamic behavior of dense fluid–solid flows in fluidized beds. In this work, the efficiency and accuracy of this model are investigated. Parameter studies are performed; in these studies, the stiffness coefficient, the fluid time step and the processor number are varied under conditions with different numbers of particles and different particle diameters. The obtained results are compared with measurements to derive the optimum parameters for CFD/DEM simulations. The results suggest that the application of higher stiffness coefficients slightly improves the simulation accuracy. However, the average computing time increases exponentially. At larger fluid time steps, the results show that the average computation time is independent of the applied fluid time step whereas the simulation accuracy decreases greatly with increasing the fluid time step. The use of smaller time steps leads to negligible improvements in the simulation accuracy but results in an exponential rise in the average computing time. The parallelization accelerates the DEM simulations if the critical number for the domain decomposition is not reached. Above this number, the performance is no longer proportional to the number of processors. The critical number for the domain decomposition depends on the number of particles. An increase in solid contents results in a shift of the critical decomposition number to higher numbers of CPUs.

Graphical abstract

Keywords

Computational fluid dynamics; Discrete element method; Stiffness coefficient; Fluid time step; Parallelization

文章导读