An analytical solution for the population balance equation using a moment method--颗粒学报PARTICUOLOGY

Yu, M., Lin, J., Cao, J., & Seipenbusch, M. (2015). An analytical solution for the population balance equation using a moment method. Particuology, 18, 194–200. https://doi.org/10.1016/j.partic.2014.06.006

An analytical solution for the population balance equation using a moment method

Mingzhou Yu ^{a b}, Jianzhong Lin ^a *, Junji Cao ^b, Martin Seipenbusch ^c

a Department of Physics, China Jiliang University, Hangzhou 310028, China
b Institute of Earth Environment, Chinese Academy of Sciences, Xi’an 710075, China
c Institute for Mechanical Processes Engineering and Mechanics, Karlsruhe Institute of Technology, Germany

10.1016/j.partic.2014.06.006

Volume 18, February 2015, Pages 194-200

Received 21 March 2014, Revised 7 June 2014, Accepted 11 June 2014, Available online 11 October 2014.

E-mail: mecjzlin@zju.edu.cn; yumz@ieecas.cn

Highlights

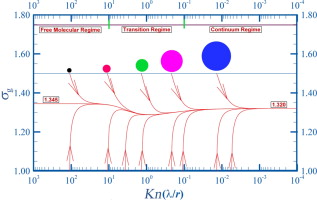
• An analytical model was proposed to solve the PBE due to Brownian coagulation.

• The model was solved analytically in free molecular and continuum regimes under some criteria.

• The model solutions were verified to be superior to existing models in efficiency and precision.

Abstract

Brownian coagulation is the most important inter-particle mechanism affecting the size distribution of aerosols. Analytical solutions to the governing population balance equation (PBE) remain a challenging issue. In this work, we develop an analytical model to solve the PBE under Brownian coagulation based on the Taylor-expansion method of moments. The proposed model has a clear advantage over conventional asymptotic models in both precision and efficiency. We first analyze the geometric standard deviation (GSD) of aerosol size distribution. The new model is then implemented to determine two analytic solutions, one with a varying GSD and the other with a constant GSD. The varying solution traces the evolution of the size distribution, whereas the constant case admits a decoupled solution for the zero and second moments. Both solutions are confirmed to have the same precision as the highly reliable numerical model, implemented by the fourth-order Runge–Kutta algorithm, and the analytic model requires significantly less computational time than the numerical approach. Our results suggest that the proposed model has great potential to replace the existing numerical model, and is thus recommended for the study of physical aerosol characteristics, especially for rapid predictions of haze formation and evolution.

Graphical abstract

Keywords

Self-preserving aerosols; Analytical solution; Taylor-expansion method of moments; Population balance equation

文章导读