A new framework for population balance modeling of spray fluidized bed agglomeration--颗粒学报PARTICUOLOGY

Hussain, M., Kumar, J., & Tsotsas, E. (2015). A new framework for population balance modeling of spray fluidized bed agglomeration. Particuology, 19, 141–154. https://doi.org/10.1016/j.partic.2014.06.005

A new framework for population balance modeling of spray fluidized bed agglomeration

Mubashir Hussain ^a *, Jitendra Kumar ^{a b}, Evangelos Tsotsas ^a

a Chair of Thermal Process Engineering, Otto-von-Guericke University Magdeburg, D-39106 Magdeburg, Germany
b Department of Mathematics, Indian Institute of Technology Kharagpur, 721302 Kharagpur, India

10.1016/j.partic.2014.06.005

Volume 19, April 2015, Pages 141-154

Received 3 March 2014, Accepted 3 June 2014, Available online 26 September 2014.

E-mail: mubashir.hussain@st.ovgu.de; mh_choudary@hotmail.com

Highlights

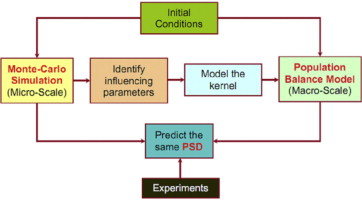
• A novel population balance model is presented for spray fluidized bed agglomeration.

• Influence of process parameters is modeled in the aggregation kinetics.

• The model is able to predict total numbers of wet particles and droplets in the system.

• The model is validated both theoretically and experimentally.

• The purposed population balance model virtually eliminates data fitting.

Abstract

Previous work (Hussain et al. (2013). Chemical Engineering Science, 101, 35) has pointed out that the conventional, one-dimensional population balance equation for aggregation can be expanded to accurately reproduce the results of discrete simulations of spray fluidized bed agglomeration. However, some parameters had to be imported from the discrete simulation (Monte-Carlo). The present paper shows how the expanded population balance can be run without importing parameters from the Monte-Carlo simulation. The expanded population balance still reproduces the results of Monte-Carlo simulations accurately, taking into account key micro-scale phenomena (sessile droplet drying, efficiency of collisions), but with much lower computational cost. Required input parameters are just the drying time of sessile droplets (calculated in advance), and the pre-factor of an equation that correlates particle collision frequency with fluidized bed expansion. In this way, the expanded population balance is, apart from autonomous, also (nearly) predictive. Its performance is demonstrated by comparisons with both Monte-Carlo results and experimental data for various operating conditions (binder mass flow rate, gas temperature). Despite formally being a one-dimensional expression, the expanded population balance captures additional properties, such as the number of wet particles and the number of droplets in the system, which are even difficult to measure in experiments.

Graphical abstract

Keywords

Population balances; Kinetics; Aggregation; Monte Carlo simulation; Fluidized bed; Modeling

文章导读