Efficient approaches of determining the motion of a spherical particle in a swirling fluid flow using weighted residual methods--颗粒学报PARTICUOLOGY

Ghasemi, S. E., Vatani, M., & Ganji, D. D. (2015). Efficient approaches of determining the motion of a spherical particle in a swirling fluid flow using weighted residual methods. Particuology, 23, 68-74. https://doi.org/10.1016/j.partic.2014.12.008

Efficient approaches of determining the motion of a spherical particle in a swirling fluid flow using weighted residual methods

Seiyed E. Ghasemi ^a *, M. Vatani ^b, D.D. Ganji ^b

a Young Researchers and Elite Club, Qaemshahr Branch, Islamic Azad University, Qaemshahr, Iran
b Department of Mechanical Engineering, Babol University of Technology, Babol, Iran

10.1016/j.partic.2014.12.008

Volume 23, December 2015, Pages 68-74

Received 25 July 2014, Revised 26 October 2014, Accepted 3 December 2014, Available online 14 April 2015, Version of Record 2 December 2015.

E-mail: ghasemi.seiyed.e@gmail.com

Highlights

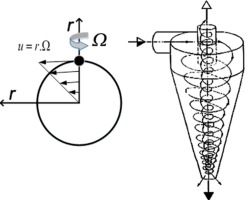
• LSM and MM were used to solve the motion of a small spherical particle in fluid forced vortex.

• Dependence of particle position and velocity on its initial values was studied.

• The results of LSM and MM were in agreement with numerical results.

Abstract

The motion of a spherical particle released in a swirling fluid flow is studied employing the least-squares method and method of moments. The governing equations are obtained and solved employing the two methods. The accuracy of the results is examined against the results of a fourth-order Runge–Kutta numerical method. The effects of various parameters, namely the initial radius, initial radial velocity, initial angular velocity, and drag-to-inertia ratio, on the non-dimensional velocity profiles and particle position distribution are considered. The results show that the radial velocity increases over time while the angular velocity decreases, and that an increase in the initial radial velocity increases the particle radial distance and angular velocity but decreases the radial velocity profile.

Graphical abstract

Keywords

Spherical particle; Swirling flow; Radial velocity; Angular velocity; Least-squares method; Method of moments

文章导读