Rolling and sliding in 3-D discrete element models--颗粒学报PARTICUOLOGY

Wang, Y., Alonso-Marroquin, F., & Guo, W. W. (2015). Rolling and sliding in 3-D discrete element models. Particuology, 23, 49-55. https://doi.org/10.1016/j.partic.2015.01.006

Rolling and sliding in 3-D discrete element models

Yucang Wang ^a *, Fernando Alonso-Marroquin ^b, William W. Guo ^a

a School of Engineering and Technology, Central Queensland University, Australia
b School of Civil Engineering, The University of Sydney, Australia

10.1016/j.partic.2015.01.006

Volume 23, December 2015, Pages 49-55

Received 25 August 2014, Revised 15 December 2014, Accepted 2 January 2015, Available online 9 May 2015, Version of Record 2 December 2015.

E-mail: yucang_wang@hotmail.com; y.wang2@cqu.edu.au

Highlights

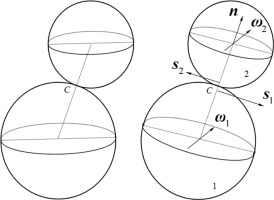
• A mistake was embedded in some models in dealing with pure sliding of differently sized particles.

• This mistake has led to wrong rolling velocity expressions when particle sizes are different.

• Clear definitions for pure rolling and sliding were made for two particles of different sizes.

• A unique solution of rolling velocity for general 3-D case has been reached.

Abstract

Rolling and sliding play fundamental roles in the deformation of granular materials. In simulations of granular flow using the discrete element method (DEM), the effect of rolling resistance at contacts should be taken into account. However, even for the simplest case involving spherical particles, there is no agreement on what is the best way to define rolling and sliding; various versions of definitions and calculations of rolling and sliding were proposed. Some even suggest that a unique definition for rolling and sliding is not possible. We re-check previous studies on rolling and sliding in DEMs and find that some researchers made a conceptual mistake when dealing with pure sliding between particles of different sizes. After considering the particle radius in the derivation of rolling velocity, the results yield a unique solution. Starting with clear and unique definitions of pure rolling and sliding, we present the detailed derivation and validate our results by checking two special cases of rolling. The decomposition of the relative motion is objective; that is, independent of the reference frame in which the relative motion is measured.

Graphical abstract

Keywords

Discrete element method; Rolling; Sliding

文章导读