Capillary bridges and capillary forces between two axisymmetric power

Wang, L., Su, F., Xu, H., Rong, W., & Xie, H. (2016). Capillary bridges and capillary forces between two axisymmetric power–law particles. Particuology, 27, 122-127. https://doi.org/10.1016/j.partic.2015.08.005

Capillary bridges and capillary forces between two axisymmetric power–law particles

Lefeng Wang, Fengting Su, Huichao Xu, Weibin Rong, Hui Xie ^*

State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China

10.1016/j.partic.2015.08.005

Volume 27, August 2016, Pages 122-127

Received 23 April 2015, Revised 21 July 2015, Accepted 18 August 2015, Available online 26 October 2015, Version of Record 14 June 2016.

E-mail: xiehui@hit.edu.cn

Highlights

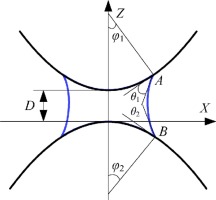
• A model for capillary force between two axisymmetric power–law profile particles was presented.

• The critical rupture criterion of the liquid bridge was shown in four forms.

• Effects of various parameters on the capillary force were demonstrated.

Abstract

Capillary interactions are fundamentally important in many scientific and industrial fields. However, most existing models of the capillary bridges and capillary forces between two solids with a mediated liquid, are based on extremely simple geometrical configurations, such as sphere–plate, sphere–sphere, and plate–plate. The capillary bridge and capillary force between two axisymmetric power–law profile particles with a mediated constant-volume liquid are investigated in this study. A dimensionless method is adopted to calculate the capillary bridge shape between two power–law profile particles based on the Young–Laplace equation. The critical rupture criterion of the liquid bridge is shown in four forms that produce consistent results. It was found that the dimensionless rupture distance changes little when the shape index is larger than 2. The results show that the power–law index has a significant influence on the capillary force between two power–law particles. This is directly attributed to the different shape profiles of power–law particles with different indices. Effects of various other parameters such as ratio of the particle equivalent radii, liquid contact angle, liquid volume, and interparticle distance on the capillary force between two power–law particles are also examined.

Graphical abstract

Keywords

Capillary force; Power–law profile particles; Power–law index; Rupture distance

文章导读