Experimental study on the 3D vibrated packing densification of binary sphere mixtures--颗粒学报PARTICUOLOGY

An, X., Li, C., & Qian, Q. (2016). Experimental study on the 3D vibrated packing densification of binary sphere mixtures. Particuology, 27, 110-114. https://doi.org/10.1016/j.partic.2015.03.009

Experimental study on the 3D vibrated packing densification of binary sphere mixtures

Xizhong An^a *, Chao Li ^b, Quan Qian ^a

a School of Materials and Metallurgy, Northeastern University, Shenyang 110004, China
b Anshan Iron and Steel Group Corporation, Yingkou 115007, China

10.1016/j.partic.2015.03.009

Volume 27, August 2016, August 2016

Pages 110-114

E-mail: anxz@mail.neu.edu.cn

Highlights

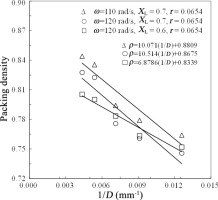
• Packing densification of binary sphere mixtures subjected to 3D mechanical vibrations was studied.

• Influences of various parameters on packing densities were investigated experimentally.

• A highest packing density of ∼0.88 was obtained, in agreement with reported results.

Abstract

The packing densification of binary spherical mixtures under 3D mechanical vibration was studied experimentally. The influences of vibration frequency (ω), volume fraction of large spheres (X_L₎, sphere size ratio (r, diameter ratio of small to large spheres), and container size (D) on the random binary packing density (ρ) were systematically analyzed. For any given set of conditions, there exist optimal ω and X_L to realize the densest random binary packing; too large or small ω and X_L is not helpful for densification. The influences of both r and D on ρ are monotonic; either reducing r or increasing D leads to a high value of ρ. With all other parameters held constant, the densest random packing occurs when X_L is dominant, which is in good agreement with the Furnas relation. Moreover, the highest random binary packing density obtained in our work agrees well with corresponding numerical and analytical results in the literature.

Graphical abstract

Keywords

Particle packing; Binary spherical mixtures; 3D vibration; Densification; Size ratio

文章导读