Representative elementary volume analysis of polydisperse granular packings using discrete element method--颗粒学报PARTICUOLOGY

Wiącek, J., & Molenda, M. (2016). Representative elementary volume analysis of polydisperse granular packings using discrete element method. Particuology, 27, 88-94. https://doi.org/10.1016/j.partic.2015.08.004

Representative elementary volume analysis of polydisperse granular packings using discrete element method

Joanna Wiącek ^*, Marek Molenda

Institute of Agrophysics, Polish Academy of Sciences, Doswiadczalna 4, 20-290 Lublin, Poland

10.1016/j.partic.2015.08.004

Volume 27, August 2016, Pages 88-94

Received 13 April 2015, Accepted 18 August 2015, Available online 25 October 2015, Version of Record 14 June 2016.

E-mail: jwiacek@ipan.lublin.pl

Highlights

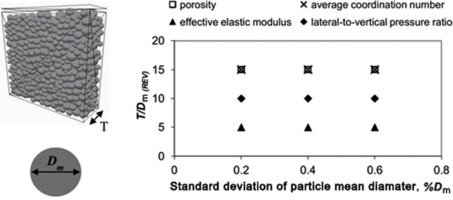
• Minimum representative elementary volume (REV) size for polydisperse granular media was studied.

• Uniaxial compression test was modeled using 3D discrete element method.

• Geometrical and mechanical REVs for sphere packings had different sizes.

• Heterogeneity of granular system had no effect on the REV size.

• Minimum REV size was found to correspond to 15 times particle mean diameter.

Abstract

The representative elementary volume (REV) for three-dimensional polydisperse granular packings was determined using discrete element method simulations. Granular mixtures of various sizes and particle size distributions were poured into a cuboid chamber and subjected to uniaxial compression. Findings showed that the minimum REV for porosity was larger compared with the REV for parameters such as coordination number, effective elastic modulus, and pressure ratio. The minimum REV for porosity and other parameters was found to equal 15, 10, and 5 times the average grain diameter, respectively. A study of the influence of sample size on energy dissipation in random packing of spheres has also confirmed that the REV size is about 15 times the average grain diameter. The heterogeneity of systems was found to have no effect on the REV for the parameters of interest for the narrow range of coefficient of uniformity analyzed in this paper. As the REV approach is commonly applied in both experimental and numerical studies, determining minimum REV size for polydisperse granular packings remains a crucial issue.

Graphical abstract

Keywords

Representative elementary volume; Polydisperse packing; Discrete element method; Sample size effect

文章导读