Lattice Boltzmann method and RANS approach for simulation of turbulent flows and particle transport and deposition--颗粒学报PARTICUOLOGY

Sajjadi, H., Salmanzadeh, M., Ahmadi, G., & Jafari, S. (2017). Lattice Boltzmann method and RANS approach for simulation of turbulent flows and particle transport and deposition. Particuology, 30, 62-72. https://doi.org/10.1016/j.partic.2016.02.004

Lattice Boltzmann method and RANS approach for simulation of turbulent flows and particle transport and deposition

H. Sajjadi ^{a b *}, M. Salmanzadeh ^a, G. Ahmadi ^b *, S. Jafari ^c

a Department of Mechanical Engineering, Shahid Bahonar University of Kerman, Kerman, Iran
b Department of Mechanical and Aeronautical Engineering, Clarkson University, Potsdam, NY, USA
c Department of Petroleum Engineering, Shahid Bahonar University of Kerman, Kerman, Iran

10.1016/j.partic.2016.02.004

Volume 30, February 2017, Pages 62-72

Received 4 July 2015, Revised 27 January 2016, Accepted 11 February 2016, Available online 5 July 2016, Version of Record 27 January 2017.

E-mail: hsajjadi@clarkson.edu; ahmadi@clarkson.edu

Highlights

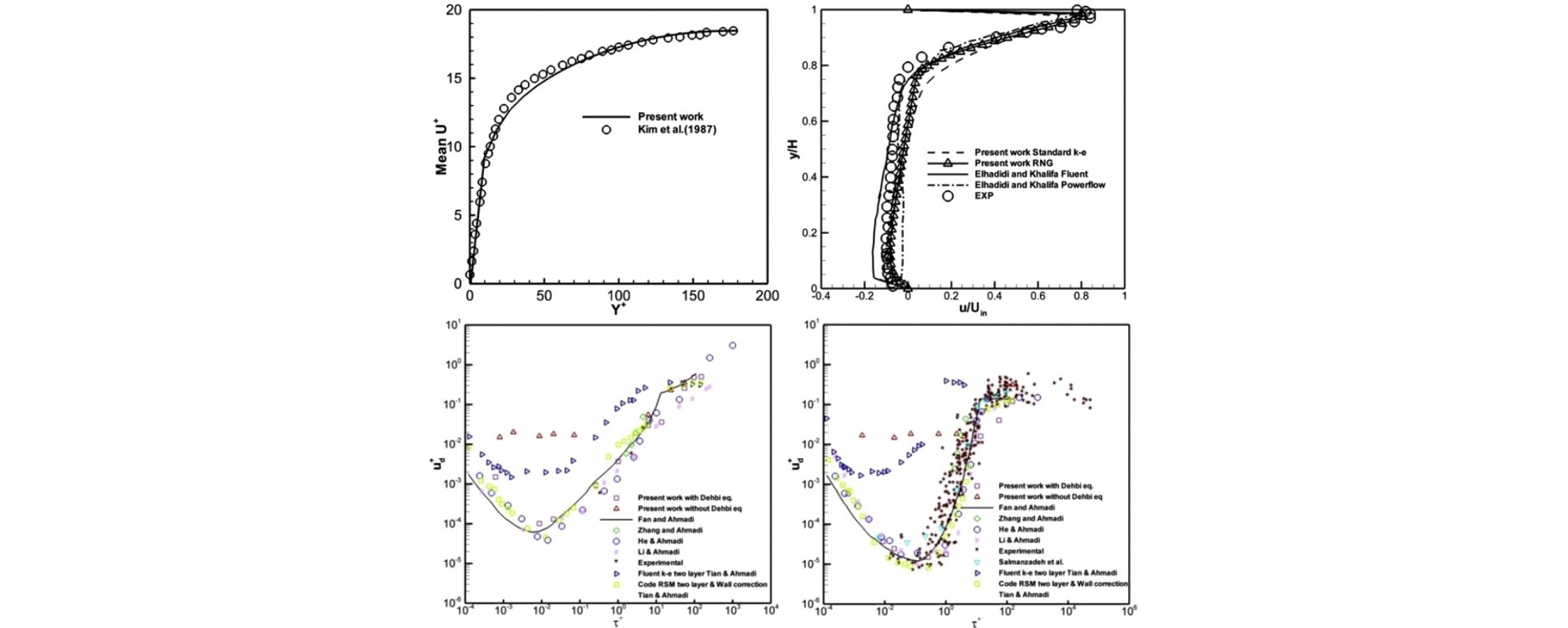
• An extended LBM approach for solving RANS equations coupled with k−ɛ turbulence model was developed.

• The simulation results were compared with available experimental data and numerical simulation.

• LBM–RANS yields a reasonably accurate description of turbulent flows at modest computational cost.

Abstract

Using the lattice-Boltzmann computational approach in conjunction with the Reynolds averaged Navier–Stokes (RANS) model, several turbulent flows and the transport and deposition of particles in different passages were studied. The new lattice Boltzmann method (LBM) solved the RANS equations coupled with the standard and renormalization group k−ɛ turbulence models. In particular, the LBM formulation was augmented by the addition of two transport equations for the probability distribution function of populations of k and ɛ. The discrete random walk model was used to generate the instantaneous turbulence fluctuations. For turbulent channel flows, the analytical fits to the root mean-square velocity fluctuations obtained by the direct numerical simulation of the turbulent flow were used in the analysis. Attention was given to the proper evaluation of the wall normal turbulent velocity fluctuations particularly near the wall. The simulation results were compared with the available numerical simulation and experimental data. The new LBM–RANS model is shown to provide a reasonably accurate description of turbulent flows and particle transport and deposition at modest computational cost.

Graphical abstract

Keywords

Lattice Boltzmann method; Reynolds averaged Navier–Stokes; Renormalization group model; k−ɛ model; Particle transport and deposition

文章导读