Modeling particle sedimentation in viscous fluids with a coupled immersed boundary method and discrete element method--颗粒学报PARTICUOLOGY

Derakhshani, S. M., Schott, D. L., & Lodewijks, G. (2017). Modeling particle sedimentation in viscous fluids with a coupled immersed boundary method and discrete element method. Particuology, 31, 191-199. https://doi.org/10.1016/j.partic.2016.09.006

Modeling particle sedimentation in viscous fluids with a coupled immersed boundary method and discrete element method

Sayed M. Derakhshani ^{a b *}, Dingena L. Schott ^a, Gabriel Lodewijks ^a

a Faculty of Mechanical, Maritime and Materials Engineering, Delft University of Technology, Delft, Netherlands
b Department of Mechanical Engineering, Faculty of Engineering, University of Isfahan, Isfahan, Iran

10.1016/j.partic.2016.09.006

Volume 31, April 2017, Pages 191-199

Received 11 November 2015, Revised 14 July 2016, Accepted 21 September 2016, Available online 16 January 2017, Version of Record 9 March 2017.

E-mail: s.m.derakhshani@tudelft.nl

Highlights

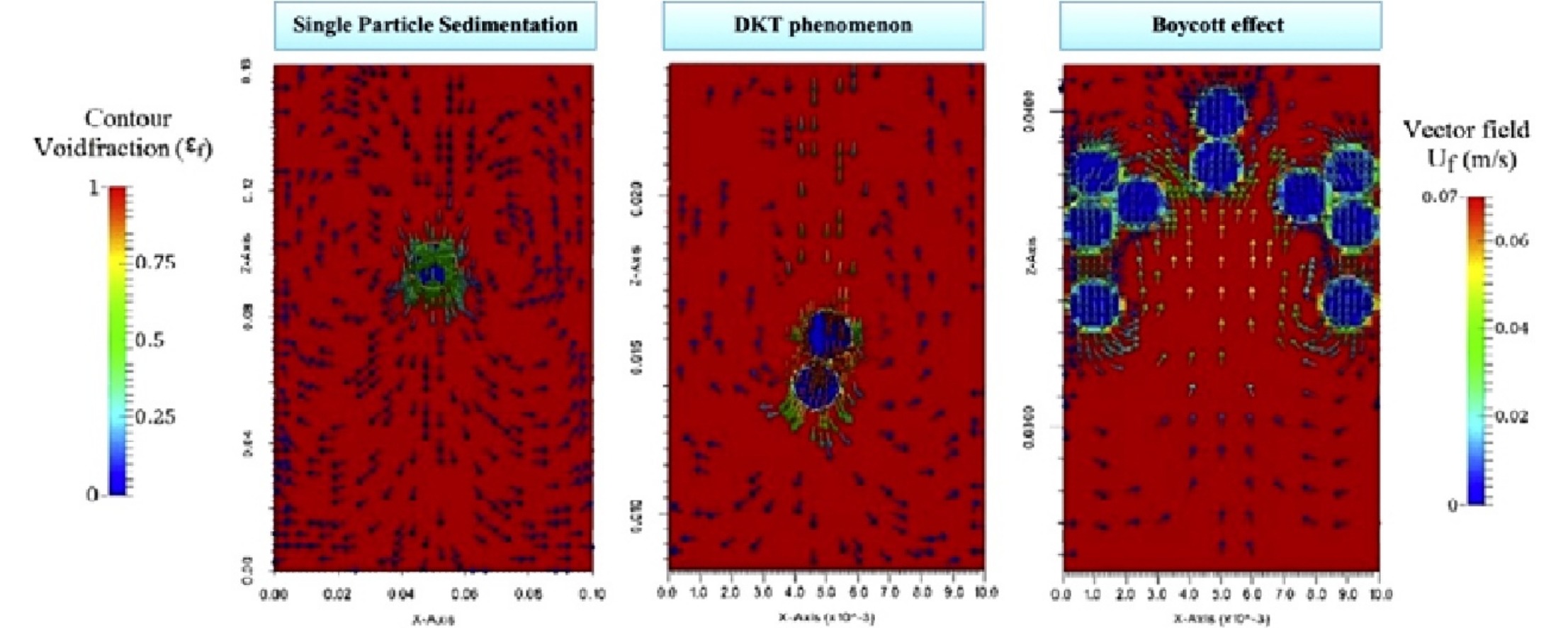
• The coupled IBM–DEM method is reliable in modeling particle sedimentation.

• A uniform CFD grid of D/dx = 4 with a local refinement of dx/4 was used in the IBM–DEM model.

• The kissing stage of the DKT process was accurately modeled with the IBM–DEM model.

• The particle sedimentation rate was maximised around α = 30° in the Boycott case study.

Abstract

Numerical techniques have increasingly been used to model fluid–particle two-phase flows. Coupling the immersed boundary method (IBM) and discrete element method (DEM) is one promising approach for modeling particulate flows. In this study, IBM was coupled with DEM to improve the reliability and accuracy of IBM for determining the positions of particles during the sedimentation process within viscous fluids. The required ratio of the particle diameter to the grid size (D/dx) was determined by comparing the simulation results with the analytical solution and experimental data. A dynamic mesh refinement model was utilised in the IBM model to refine the computational fluid dynamics grid near the particles. In addition, an optimum coupling interval between the IBM and DEM models was determined based on the experimental results of a single particle sedimentation within silicon oil at a Reynolds number of 1.5. The experimental results and the analytical solution were then utilised to validate the IBM–DEM model at Reynolds numbers of 4.1, 11.6, and 31.9. Finally, the validated model was utilised to investigate the sedimentation process for more than one particle by modeling the drafting-kissing-tumbling process and the Boycott phenomenon. Benchmark tests showed that the IBM–DEM technique preserves the advantages of DEM for tracking a group of particles, while the IBM provides a reliable and accurate approach for modeling the particle–fluid interaction.

Graphical abstract

Keywords

Immersed boundary method; Discrete element method; Particle sedimentation; Boycott phenomenon

文章导读