A Markov chain model of mixing kinetics for ternary mixture of dissimilar particulate solids--颗粒学报PARTICUOLOGY

Mizonov, V., Balagurov, I., Berthiaux, H., & Gatumel, C. (2017). A Markov chain model of mixing kinetics for ternary mixture of dissimilar particulate solids. Particuology, 31, 80-86. https://doi.org/10.1016/j.partic.2016.05.006

A Markov chain model of mixing kinetics for ternary mixture of dissimilar particulate solids

Vadim Mizonov ^a *, Ivan Balagurov ^a, Henri Berthiaux ^b, Cendrine Gatumel ^b

a Department of Applied Mathematics, Ivanovo State Power Engineering University, Russia
b Centre RAPSODEE, UMR CNRS 5302, Ecole des Mines d’Albi-Carmaux, Campus Jarlard, Route de Teillet, 81000 Albi, France

10.1016/j.partic.2016.05.006

Volume 31, April 2017, Pages 80-86

Received 21 March 2016, Revised 28 April 2016, Accepted 12 May 2016, Available online 28 August 2016, Version of Record 9 March 2017.

E-mail: mizonov46@mail.ru

Highlights

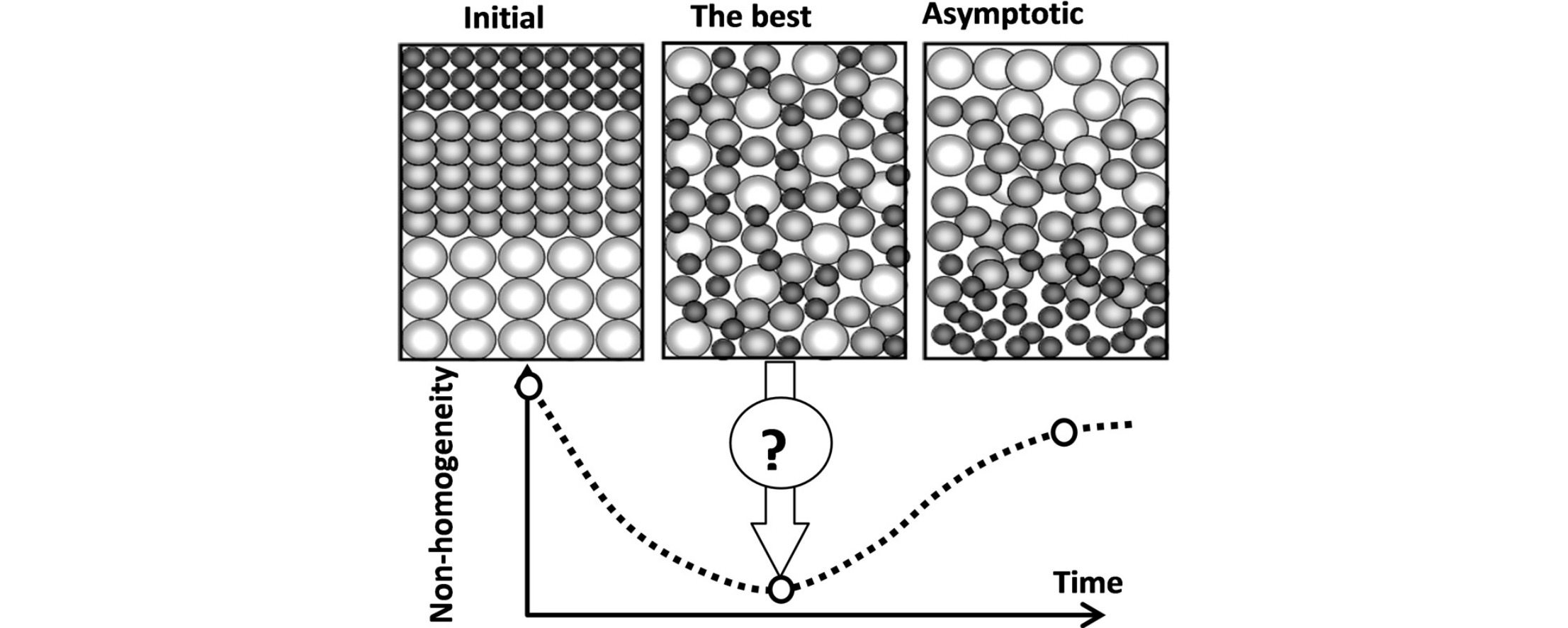
• A Markov chain model of mixing glass beads of three dissimilar diameters was proposed.

• Optimum mixing time for entire mixture did not coincide with that of individual components.

• The model was experimentally validated.

• Combining the model with DEM simulation may improve its efficiency at low computational time.

Abstract

This paper presents a simple but informative mathematical model to describe the mixing of three dissimilar components of particulate solids that have the tendency to segregate within one another. A nonlinear Markov chain model is proposed to describe the process. At each time step, the exchange of particulate solids between the cells of the chain is divided into two virtual stages. The first is pure stochastic mixing accompanied by downward segregation. Upon the completion of this stage, some of the cells appear to be overfilled with the mixture, while others appear to have a void space. The second stage is related to upward segregation. Components from the overfilled cells fill the upper cells (those with the void space) according to the proposed algorithm. The degree of non-homogeneity in the mixture (the standard deviation) is calculated at each time step, which allows the mixing kinetics to be described. The optimum mixing time is found to provide the maximum homogeneity in the ternary mixture. However, this “common” time differs from the optimum mixing times for individual components. The model is verified using a lab-scale vibration vessel, and a reasonable correlation between the calculated and experimental data is obtained.

Graphical abstract

Keywords

Ternary mixture; Segregation; Mixing kinetics; Markov chain; Matrix of transition probabilities; Optimum mixing time

文章导读