Kinematics and dynamics of a particle on a non-simple harmonic vibrating screen--颗粒学报PARTICUOLOGY

Wang, L., Ding, Z., Meng, S., Zhao, H., & Song, H. (2017). Kinematics and dynamics of a particle on a non-simple harmonic vibrating screen. Particuology, 32, 167-177. https://doi.org/10.1016/j.partic.2016.11.002

Kinematics and dynamics of a particle on a non-simple harmonic vibrating screen

Lijun Wang ^a *, Zhenjun Ding ^a, Shuang Meng ^b, Huijun Zhao ^a, Huiqiang Song ^a

a College of Engineering, Northeast Agricultural University, Harbin 150030, China
b Light Industry School, Harbin University of Commerce, Harbin 150028, China

10.1016/j.partic.2016.11.002

Volume 32, June 2017, Pages 167-177

Received 27 October 2015, Revised 5 October 2016, Accepted 7 November 2016, Available online 28 March 2017, Version of Record 20 April 2017.

E-mail: wanglijun@neau.edu.cn

Highlights

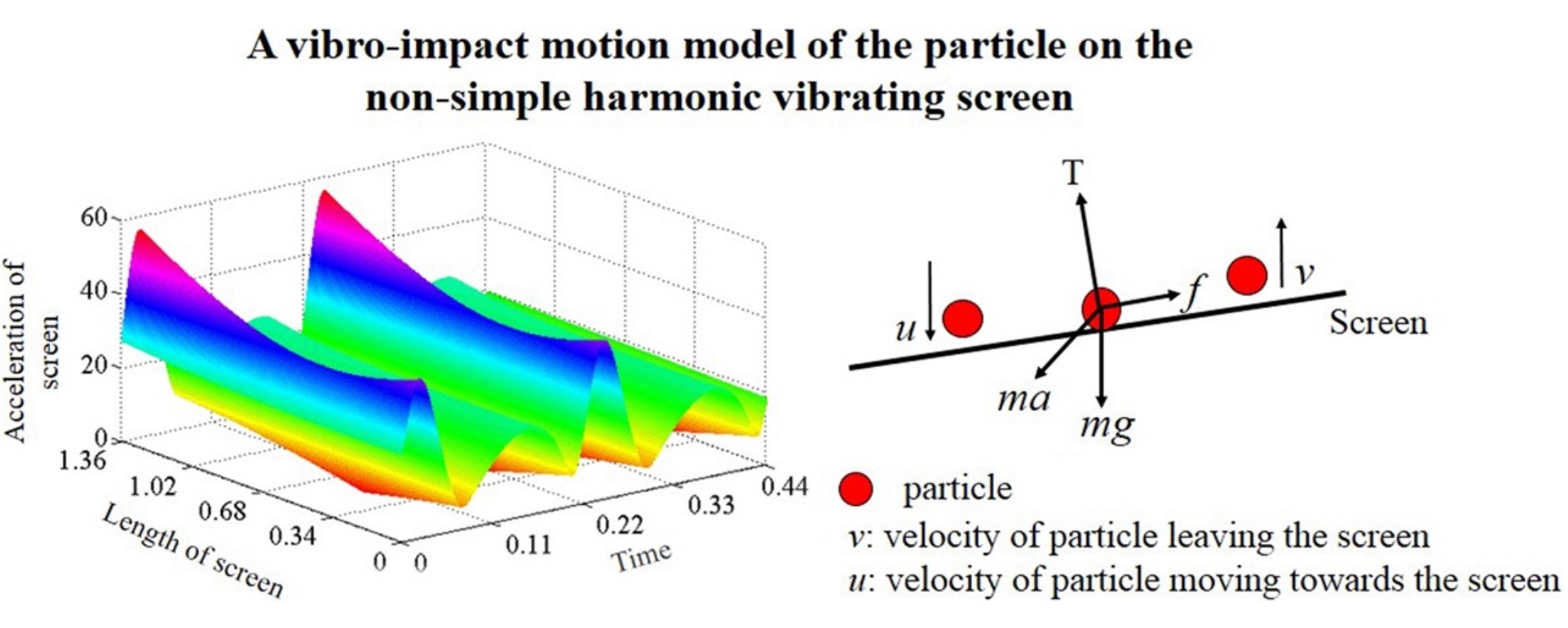
• A mathematical model was established to analyze motion of a planar reciprocating vibrating screen.

• The motion of the screen was simulated numerically and analyzed using MATLAB.

• The actual motion of the screen is the non-simple harmonic motion.

• The screen’ angle was varied caused by its multiple harmonic motions.

• The behaviors of particle in the different regions of the screen were obtained.

Abstract

The motion of a particle on a screen is directly affected by the motion of the screen if airflow and intergranular friction are ignored. To study this effect, a mathematical model was established to analyze the motion of a planar reciprocating vibrating screen, and a matrix method was employed to derive its equation of motion. The motion of the screen was simulated numerically and analyzed using MATLAB. The results show that the screen undergoes non-simple harmonic motion and the law of motion of each point in the screen is different. The tilt angle of the screen during screening is not constant but varies according to a specific periodic function. The results of numerical simulations were verified through experiments. A high-speed camera was used to track the motion of three points in the longitudinal direction of the screen. The balance equation for forces acting on a single particle on the screen was derived based on the non-simple harmonic motion of the screen. These forces were simulated using MATLAB. Different types of particle motion like slipping forward, moving backward, and being tossed to different parts of the screen were analyzed. A vibro-impact motion model for a particle on the non-simple harmonic vibrating screen was established based on the nonlinear law of motion of the particle. The stability of fixed points of the map is discussed. Regimes of different particle behaviors such as stable periodic motion, period-doubling bifurcation motion, Hopf bifurcation motion, and chaotic motion were obtained. With the actual law of motion of the screen and the behavior of a particle on the screen, a theoretical basis for design optimization of the screen is provided.

Graphical abstract

Keywords

Vibrating screen; Non-simple harmonic motion; Particle screening; Kinematics and dynamics; Numerical simulation

文章导读