Bonded-particle model calibration using response surface methodology--颗粒学报PARTICUOLOGY

Chehreghani, S., Noaparast, M., Rezai, B., & Shafaei, S. Z. (2017). Bonded-particle model calibration using response surface methodology. Particuology, 32, 141-152. https://doi.org/10.1016/j.partic.2016.07.012

Bonded-particle model calibration using response surface methodology

Sajjad Chehreghani ^a *, Mohammad Noaparast ^a, Bahram Rezai ^b, Sied Ziaedin Shafaei ^a

a School of Mining, University College of Engineering, University of Tehran, 14395-515, Tehran, Iran
b Department of Mining and Metallurgy Engineering, Amir Kabir University of Technology, Tehran, Iran

10.1016/j.partic.2016.07.012

Volume 32, June 2017, Pages 141-152

Received 16 December 2015, Revised 25 June 2016, Accepted 29 July 2016, Available online 6 March 2017, Version of Record 20 April 2017.

E-mail: s.chehreghani@ut.ac.ir

Highlights

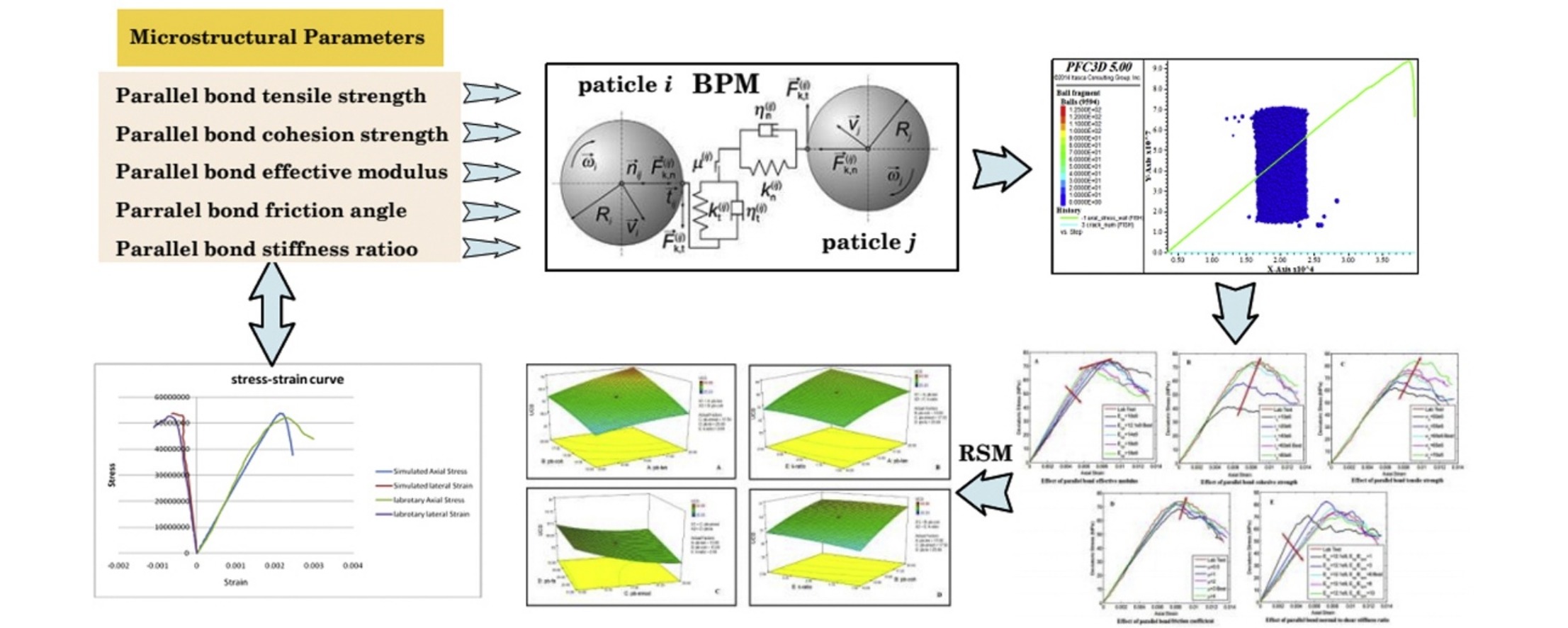
• RSM and CCD were used to analyze the effects of microparameters in a BPM calibration process.

• Elasticity modulus was highly correlated to the parallel bond effective modulus.

• Both parallel bond tensile and cohesion strengths had considerable effects on UCS.

Abstract

The bonded-particle model (BPM) is commonly used in numerical analysis of the mechanical behavior of rock samples. Constructing a BPM model requires specification of a number of microstructural parameters, including the parallel-bond tensile strength, parallel-bond cohesion strength, parallel-bond effective modulus, parallel-bond friction angle, and parallel-bond stiffness ratio. These parameters cannot be easily measured in the laboratory or directly related to either measurable or physical material parameters. Hence, a calibration process is required to choose the values to be used in simulations of physical systems. In this study, response surface methodology along with the central composite design approach is used to calibrate BPMs. The sensitivities of the microparameters related to the uniaxial compressive strength (UCS) and elasticity modulus (i.e., the macroscopic responses of the models) are thoroughly scrutinized. Numerical simulations are performed to carefully assess the performance of the model. It is found that the elasticity modulus is highly correlated with the parallel-bond effective modulus. In addition, the parallel-bond tensile and cohesion strengths are the two most significant microparameters with a considerable effect on the UCS. The predicted values determined by the proposed approach are in good agreement with the observed values, which verifies the applicability of the proposed method.

Graphical abstract

Keywords

Bonded-particle model; Calibration; Response surface methodology; Uniaxial compressive strength

文章导读