Discrete and continuum modeling of granular flow in silo discharge--颗粒学报PARTICUOLOGY

Tian, T., Su, J., Zhan, J., Geng, S., Xu, G., & Liu, X. (2018). Discrete and continuum modeling of granular flow in silo discharge. Particuology, 36, 127-138. https://doi.org/10.1016/j.partic.2017.04.001

Discrete and continuum modeling of granular flow in silo discharge

Tian Tian ^{a b c}, Jinglin Su ^a, Jinhui Zhan ^a, Shujun Geng ^{a b}, Guangwen Xu ^a *, Xiaoxing Liu ^{a b *}

a State Key Laboratory of Multi-Phase Complex System, Institute of Process Engineering, Chinese Academy of Science, Beijing 100190, China
b University of Chinese Academy of Sciences, Beijing 100049, China
c Sino-Danish Center for Education and Research, Beijing 100190, China

10.1016/j.partic.2017.04.001

Volume 36, February 2018, Pages 127-138

Received 15 February 2017, Revised 17 March 2017, Accepted 5 April 2017, Available online 17 July 2017, Version of Record 22 December 2017.

E-mail: gwxu@ipe.ac.cn; xxliu@ipe.ac.cn

Highlights

• Flow mode transition of granular material in a flat-bottomed silo was studied.

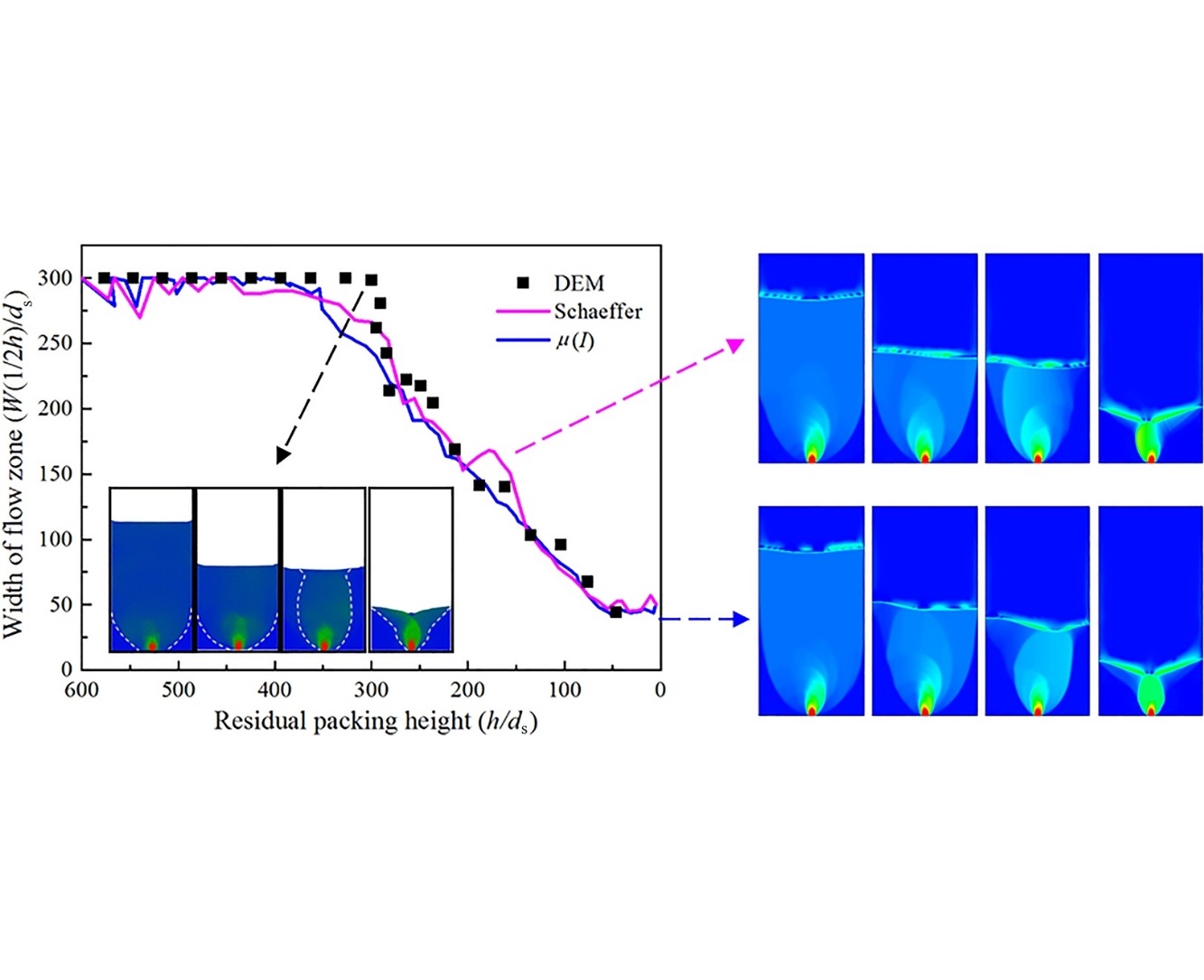
• The evolution of flowing zone width showed a history-dependent characteristic.

• Both Schaeffer and μ(I) model can predict the flow patterns given by DEM simulations.

• S–S model gave a consistent type B flow mode.

• All the three considered frictional viscosity models over-estimated the discharge rate.

Abstract

Granular material discharge from a flat-bottomed silo has been simulated by using continuum modeling and a three-dimensional discrete-element method (DEM). The predictive abilities of three commonly used frictional viscosity models (Schaeffer, S–S, and μ(I)) were evaluated by comparing them with the DEM data. The funnel-flow pattern (type C) and the semi-mass-flow pattern (type B) that was predicted by DEM simulations can be represented when the Schaeffer or μ(I) model is used, whereas the S–S model gives a consistent type-B flow pattern. All three models over-estimate the discharge rate compared with the DEM. The profiles of the solids volume fraction and the vertical velocity above the outlet show that the larger discharge rates given by the Schaeffer and μ(I) model result from an over-estimation of volume fraction, whereas the deviation in the S–S model stems from the failure to predict a solid vertical velocity and a volume fraction.

Graphical abstract

Keywords

Silo; Flow pattern; Discharge rate; Discrete-element model; Frictional viscosity model

文章导读