A regularization algorithm for estimating the multimodal size distribution of nanoparticles from multiangle dynamic light scattering--颗粒学报PARTICUOLOGY

Li, L., Yang, K., Li, W., Li, K., Yu, L., & Xia, M. (2018). A regularization algorithm for estimating the multimodal size distribution of nanoparticles from multiangle dynamic light scattering. Particuology, 41, 30-39. https://doi.org/10.1016/j.partic.2017.12.015

A regularization algorithm for estimating the multimodal size distribution of nanoparticles from multiangle dynamic light scattering

Lei Li ^{a b}, Kecheng Yang ^a, Wei Li ^a, Kai Li ^a, Long Yu ^a, Min Xia ^a *

a School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China
b Wuhan University Scientific Journals Press, Wuhan 430072, China

10.1016/j.partic.2017.12.015

Volume 41, December 2018, Pages 30-39

Received 10 October 2017, Revised 8 December 2017, Accepted 13 December 2017, Available online 15 June 2018, Version of Record 1 November 2018.

E-mail: xiamin@hust.edu.cn

Highlights

• A modified self-adaptive algorithm was proposed to retrieve PSDs from MDLS measurement data.

• The algorithm chose appropriate regularization methods in iterative recursion.

• The algorithm reconstructed the PSDs more precisely.

• Numerical and experimental results proved the good anti-noise performance of the algorithm.

Abstract

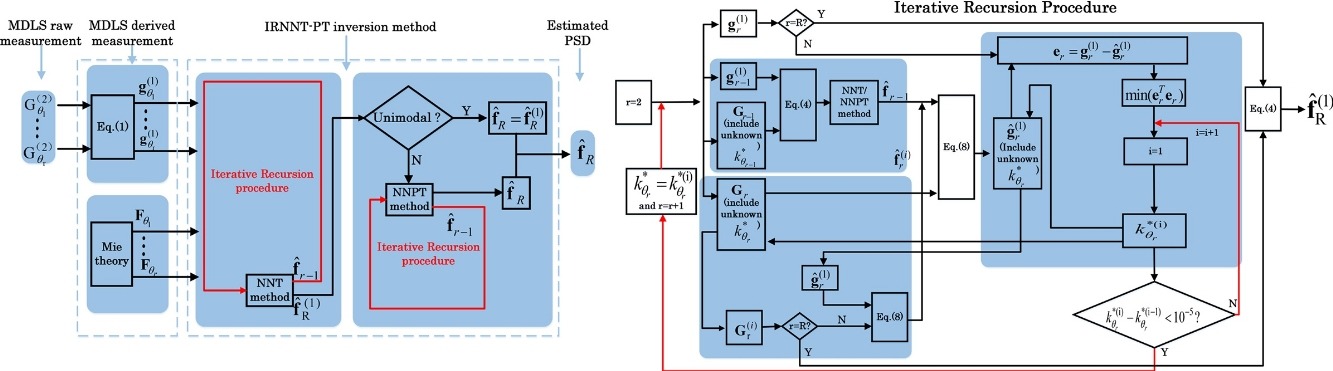
The multiangle dynamic light scattering (MDLS) technique provides more robust, reproducible, and accurate particle size distributions (PSDs) than single-angle dynamic light scattering. However, in MDLS, the determination of peak locations is difficult but significant, particularly for multimodal distributions. In this paper, a self-adaptive algorithm, the iterative recursion nonnegative Tikhonov–Phillips–Twomey (IRNNT-PT) algorithm, is proposed for the estimation of the PSD from MDLS measurements. This algorithm optimizes the weighting coefficients, distinguishes features of PSDs and chooses the optimal inversion method from two regularization algorithms self-adaptively. Numerical simulations and experimental results for unimodal and multimodal distributions are presented to demonstrate both the validity and noise immunity of the IRNNT-PT algorithm, and demonstrate that the proposed algorithm can be well applied to reconstruct PSDs from MDLS measurements.

Graphical abstract

Keywords

Dynamic light scattering; Particle size distribution; Inverse scattering; Mie theory; Scattering measurements

文章导读