Three-dimensional reconstruction of a point immersed in water and application to a single rising bubble--颗粒学报PARTICUOLOGY

Li, S., Chen, L., & Sun, Z. (2019). Three-dimensional reconstruction of a point immersed in water and application to a single rising bubble. Particuology, 46, 83-92. https://doi.org/10.1016/j.partic.2018.08.015

Three-dimensional reconstruction of a point immersed in water and application to a single rising bubble

Saiwei Li, Luyang Chen, Zhiqiang Sun ^*

School of Energy Science and Engineering, Central South University, Changsha 410083, China

10.1016/j.partic.2018.08.015

Volume 46, October 2019, Pages 83-92

Received 18 November 2017, Revised 4 April 2018, Accepted 8 August 2018, Available online 5 June 2019, Version of Record 8 August 2019.

E-mail: zqsun@csu.edu.cn

Highlights

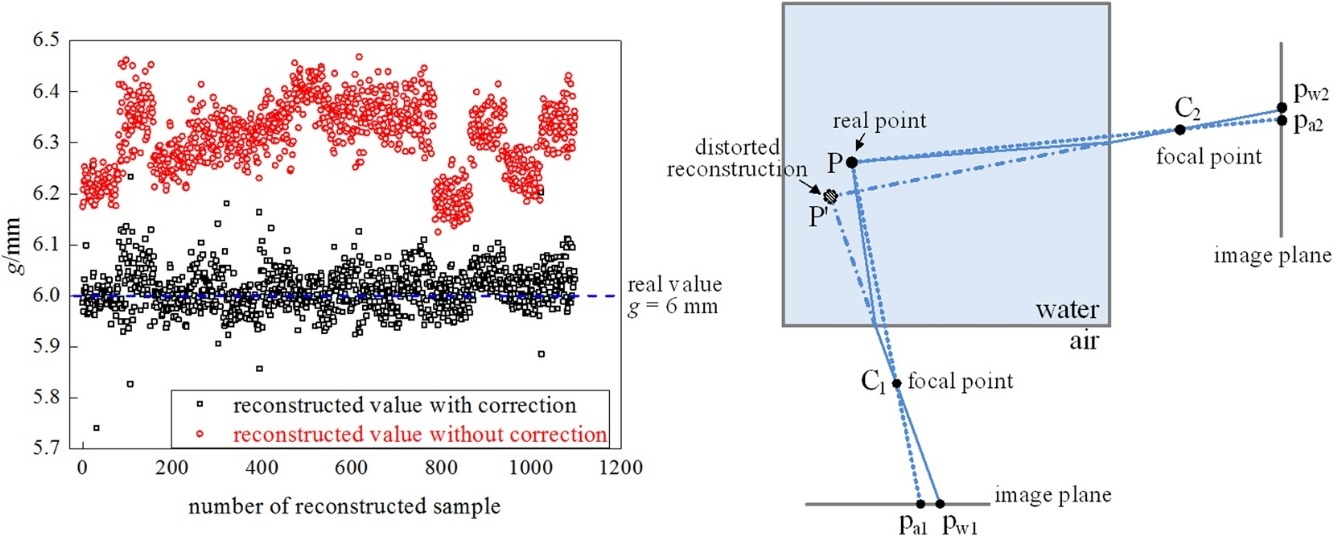
• Reconstructed image of submerged objects is falsely enlarged because of refraction.

• Proposed correction method accounts for refraction during reconstruction.

• Method was validated by reconstructing a checkerboard in water with good accuracy.

• Method was applied to reconstructing the trajectory of a single rising bubble.

Abstract

The ability to reconstruct an object submerged in water is instrumental in scenarios such as the study of a rising bubble trajectory, and subsequently, its motion and force balance. In this paper, we propose a method that can reconstruct the three-dimensional position of a scene point immersed in water, while taking into account the refraction-induced distortion at the air–water interface between the point and camera. The scene point is captured by two orthogonally placed high-speed cameras, providing a pair of images through which the point’s image coordinates are obtained. With pre-calibrated camera matrices, the world coordinates of the point’s position can be correctly calculated using a triangulation method, provided the scene point is in air. However, because of refraction, triangulating the image pairs of the point submerged in water results in erroneous world coordinates. Thus, we propose a method to correct the point’s image coordinates to account for refraction induced distortion during reconstruction. The method was first verified by reconstructing the coordinates of square corners on a checkerboard, which produced results that deviated from the real value by 0.18%, as opposed to the 5.15% false enlargement prior to correction. Then, we applied the method to the reconstruction of the three-dimensional trajectories of single rising spherical bubbles, whose results were in favorable agreement with previous studies.

Graphical abstract

Keywords

Underwater visualization; Three-dimensional reconstruction; Refraction; Distortion correction

文章导读