Game-theoretical explorations of the mesoscale flow structure and regime transitions in bubble columns--颗粒学报PARTICUOLOGY

Yuan, S., Mu, Y., Guan, X., Liu, Z., Chen, J., Yang, N., & Zhang, L. (2020). Game-theoretical explorations of the mesoscale flow structure and regime transitions in bubble columns. Particuology, 48, 100-108. https://doi.org/10.1016/j.partic.2018.09.008

Game-theoretical explorations of the mesoscale flow structure and regime transitions in bubble columns

Shuo Yuan ^{a b}, Yifen Mu ^a *, Xiaoping Guan ^c, Zhixin Liu ^{a b}, Jianhua Chen ^c, Ning Yang ^c, Lin Zhang ^c

a Key Lab of Systems and Control, Institute of Systems Sciences, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
b University of Chinese Academy of Sciences, Beijing 100049, China
c State Key Laboratory of Multiphase Complex Systems, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China

10.1016/j.partic.2018.09.008

Volume 48, February 2020, Pages 100-108

Received 29 June 2018, Revised 3 September 2018, Accepted 5 September 2018, Available online 25 March 2019, Version of Record 27 January 2020.

E-mail: mu@amss.ac.cn

Highlights

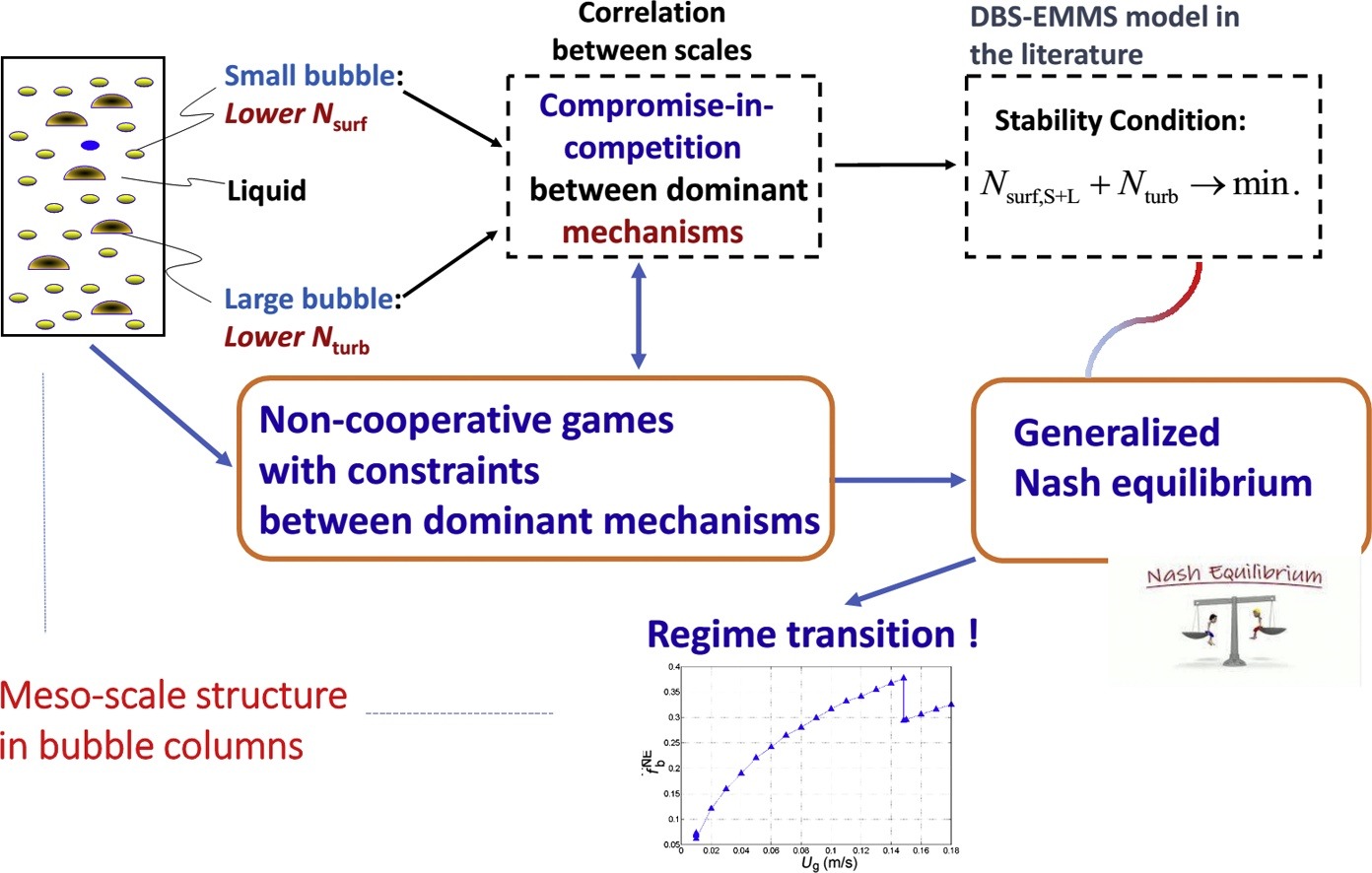
• Noncooperative game model with constraints is built between small and large bubbles.

• Generalized Nash equilibrium (GNE) is defined and computed as stable system state.

• System at GNE reveals regime transition and critical point of gas velocity.

• GNE results reveal single-bubble dominant mechanism with increasing gas velocity.

Abstract

Understanding the mesoscale structure and regime transition in bubble columns is of great significance for reactor design and scaleup. Based on the energy-minimization multiscale (EMMS) model, a noncooperative game model with constraints is proposed to investigate the structural properties of gas–liquid systems in which small and large bubbles are chosen as players and the energy consumption form the objective function. The conservation equations of the system can be regarded as the constraints of the game. For the formulated noncooperative game model, the concept of the generalized Nash equilibrium (GNE) is used to characterize the solution. An algorithm is developed to numerically compute the GNE and some important structural parameters in the system. The numerical results show the existence of the GNE for all values of the superficial gas velocity U_g. As U_g varies, the trends in the state variables can be observed and the critical point of U_g identified. The overall trend of the flow regime transition agrees with the original EMMS model and experimental results, although the GNE calculation also reveals different single-bubble dominant mechanisms with increasing U_g.

Graphical abstract

Keywords

Bubble column; Mesoscale; Regime transition; Game theory; Generalized Nash equilibrium; EMMS model

文章导读