Pressure recovery characteristics for a dilute gas–particle suspension flowing vertically downward in a pipe with a sudden expansion: A two-fluid modeling approach--颗粒学报PARTICUOLOGY

Senapati, S. K., & Dash, S. K. (2020). Pressure recovery characteristics for a dilute gas–particle suspension flowing vertically downward in a pipe with a sudden expansion: A two-fluid modeling approach. Particuology, 50, 100-111. https://doi.org/10.1016/j.partic.2019.07.001

Pressure recovery characteristics for a dilute gas–particle suspension flowing vertically downward in a pipe with a sudden expansion: A two-fluid modeling approach

Santosh Kumar Senapati ^*, Sukanta Kumar Dash

Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, West Bengal 721302, India

10.1016/j.partic.2019.07.001

Volume 50, June 2020, Pages 100-111

Received 2 March 2019, Revised 28 May 2019, Accepted 30 July 2019, Available online 10 September 2019, Version of Record 7 April 2020.

E-mail: senapatis431@gmail.com

Highlights

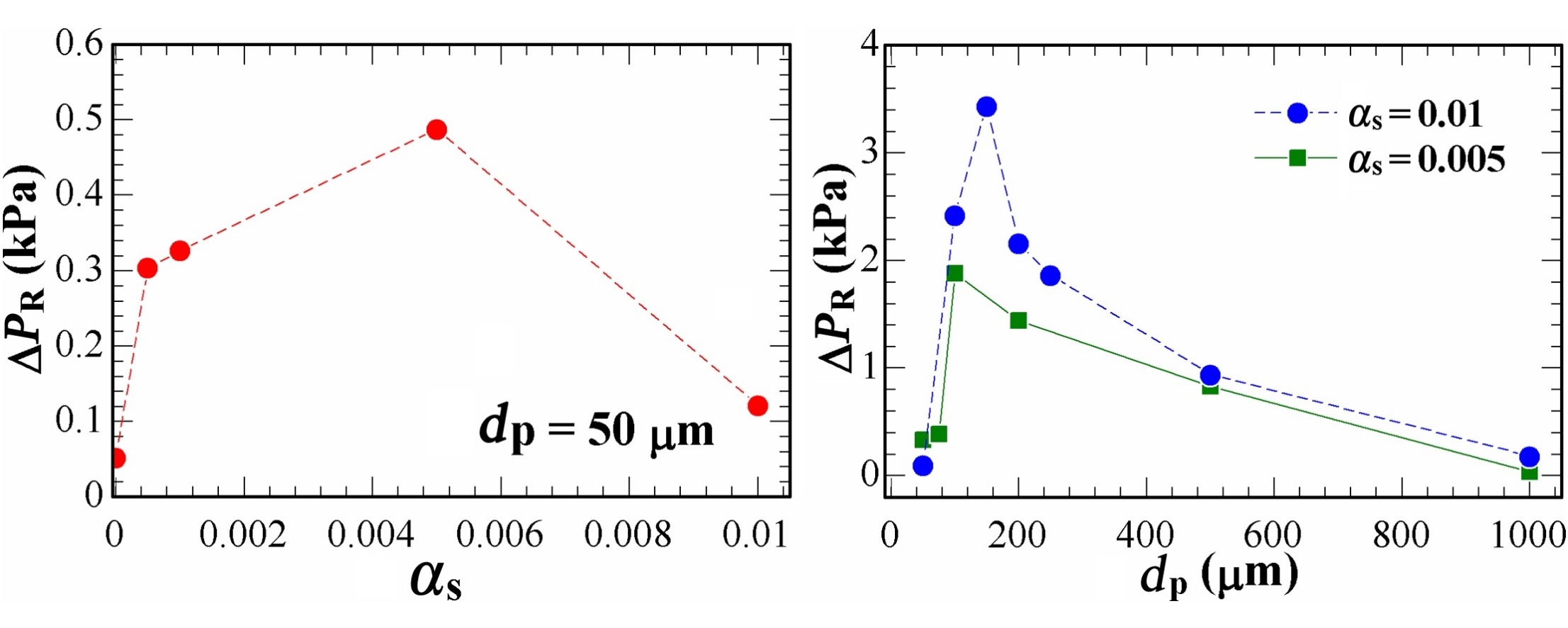
• Pressure recovery of gas–solid suspension is studied at higher limits of dilute phase flow.

• Particle–particle and particle–wall collisions affect pressure recovery.

• Dilute phase flows at higher limits especially with fine particles exhibit a critical volume fraction and critical diameter.

• Above and below criticality, pressure recovery shows completely opposite trends.

Abstract

This work applies the Eulerian‒Eulerian model in conjunction with the kinetic theory of granular flow and inter-particle collisions to study the characteristics of pressure recovery for a dilute gas–particle suspension flowing through a pipe with a sudden expansion at a relatively higher solid loading. To do so, the numerical procedure was validated against experimental results for relatively small dilute phase flows in a pipe with a sudden expansion; a satisfactory agreement was obtained. Initially, the effect of the two significant numerical parameters namely, the speculairty coefficient and the coefficient of restitution for particle–particle collisions were investigated and then, for fixed combinations of these parameters the effect of particle-phase volume fraction, particle density, particle size, and inlet slip ratio were studied. It was concluded that pressure recovery diminishes as the speculairty coefficient increases and the particle–particle coefficient of restitution decreases. Pressure recovery was found to increase with increasing solid volume fraction for coarse particles whereas, for fine particles, a critical volume fraction is obtained above which pressure recovery reduces. An increase in slip ratio is found to diminish pressure recovery. Similarly, at relatively higher solid volume fractions, a critical diameter was found, above and below which pressure recovery decreases.

Graphical abstract

Keywords

Gas‒solid flow; Sudden expansion pipe; Eulerian‒Eulerian model; Pressure recovery; Vertically downward flow

文章导读