Two-fluid modelling for cylindrical fluidized beds using kinetic theory for rough spheres--颗粒学报PARTICUOLOGY

Yang, L., Padding, J. T., & Kuipers, J. A. M. (2020). Two-fluid modelling for cylindrical fluidized beds using kinetic theory for rough spheres. Particuology, 50, 25-34. https://doi.org/10.1016/j.partic.2019.05.006

Two-fluid modelling for cylindrical fluidized beds using kinetic theory for rough spheres

Lei Yang ^a *, J.T. Padding ^b, J.A.M. Kuipers ^c

a Helmholtz Institute Erlangen-Nürnberg for Renewable Energy (IEK-11), Fürther Straße 248, 90429 Nürnberg, Germany
b Department of Process and Energy, Delft University of Technology, 2628CB Delft, The Netherlands
c Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, 5600MB Eindhoven, The Netherlands

10.1016/j.partic.2019.05.006

Volume 50, June 2020, Pages 25-34

Received 28 September 2018, Revised 30 April 2019, Accepted 14 May 2019, Available online 5 August 2019, Version of Record 7 April 2020.

E-mail: le.yang@fz-juelich.de

Highlights

• Extended KTGF is first implemented in three-dimensional cylindrical coordinates.

• Anti-symmetric part of the velocity gradient in the solids stress tensor is included.

• Implementation verified by comparing results from present model and original model.

• Extended KTGF predicts similar solids distribution and circulation pattern.

• Extended KTGF gives improved predictions for the temporal bubble behavior.

Abstract

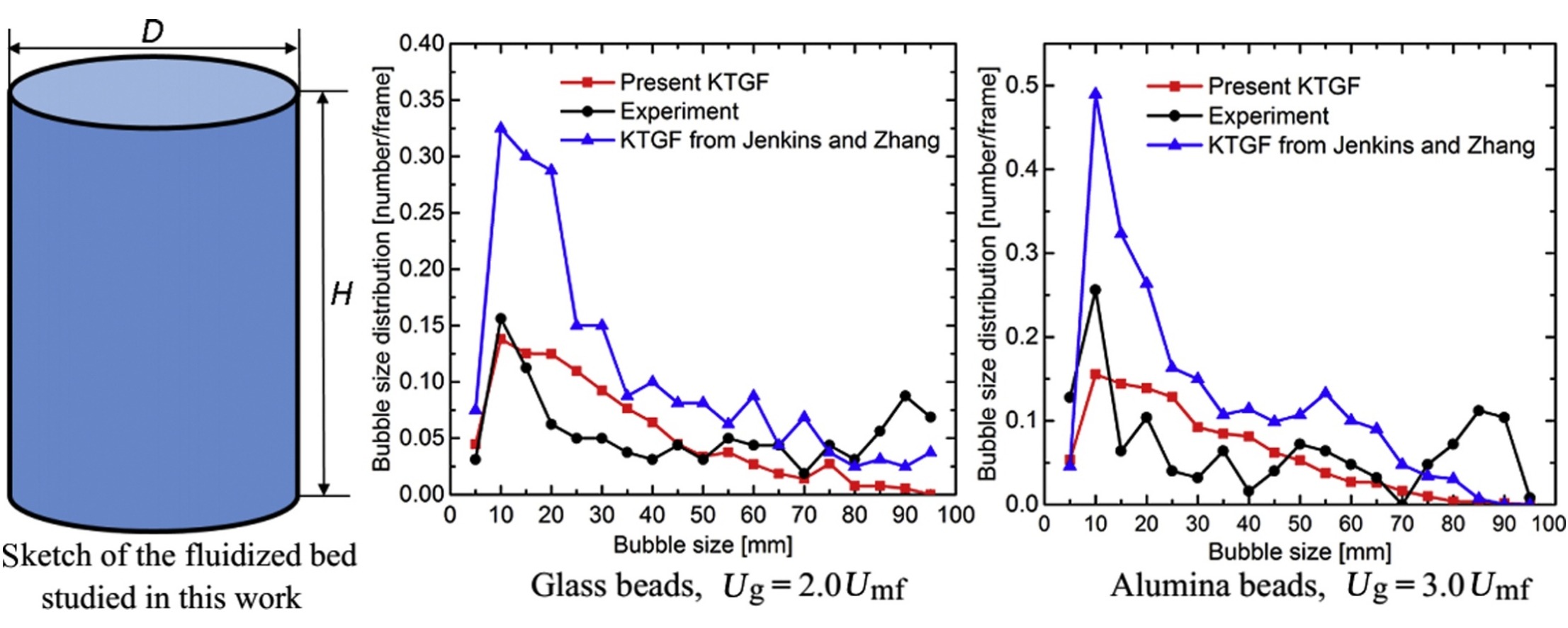
Recently, we have extended the kinetic theory of granular flow (KTGF) to include friction between the spherical particles and tested it in rectangular geometries. In this study, the extended KTGF implemented in cylindrical coordinates is used to model the more-commonly employed cylindrical bubbling fluidized beds. Special attention is paid to the anti-symmetric part of the velocity gradient in the solids stress tensor. For verification of the implementation, a comparison of the present model in the limit of zero friction with the original (frictionless) KTGF model was made. Subsequently, simulations of bubbling fluidized beds of inelastic particles were performed using our extended KTGF and an effective KTGF model for inelastic particles of Jenkins and Zhang. The simulation results show good agreement for the time-averaged solids volume fraction distribution and solids circulation patterns. Finally, our model is validated by predicting the individual bubble behavior in dense bubbling fluidized beds containing different granular materials in a comparison with experimental data from Verma et al. (2014). The extended KTGF leads to an improved agreement with experimental bubble data. Compared to previous work (Yang et al., 2016b, 2017c), and by introducing cylindrical coordinates, the current work demonstrates that the extended KTGF improves predictions for the temporal bubble behavior of cylindrical fluidized beds.

Graphical abstract

Keywords

Fluidization; Frictional collision; Rough particles; Cylindrical bed hydrodynamics; Two-fluid model

文章导读