EMMS drag model for simulating a gas–solid fluidized bed of geldart B particles: Effect of bed model parameters and polydisperity--颗粒学报PARTICUOLOGY

Kshetrimayum, K. S., Park, S., Han, C., & Lee, C.-J. (2020). EMMS drag model for simulating a gas–solid fluidized bed of geldart B particles: Effect of bed model parameters and polydisperity. Particuology, 51, 142-154. https://doi.org/10.1016/j.partic.2019.10.004

EMMS drag model for simulating a gas–solid fluidized bed of geldart B particles: Effect of bed model parameters and polydisperity

Krishnadash S. Kshetrimayum ^a, Seongho Park ^b, Chonghun Han^b, Chul-Jin Lee ^a *

a School of Chemical Engineering and Materials Science, Chung-Ang University, 06974 Seoul, South Korea
b School of Chemical and Biological Engineering, Seoul National University, San 56-1, Shillim-dong, Kwanak-gu, Seoul, 151-742, South Korea

10.1016/j.partic.2019.10.004

Volume 51, August 2020, Pages 142-154

Received 13 February 2018, Revised 11 September 2019, Accepted 7 October 2019, Available online 26 December 2019, Version of Record 11 April 2020.

E-mail: cjlee@cau.ac.kr

Highlights

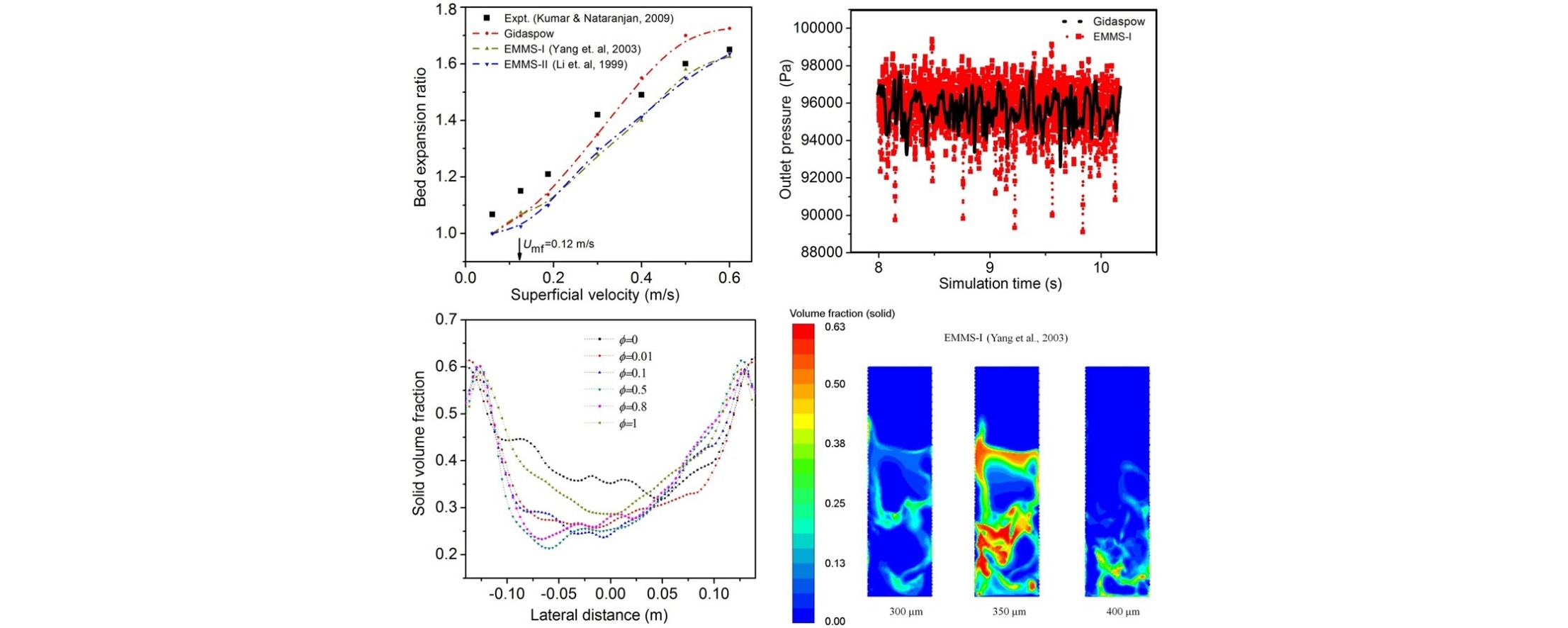
• Gas–solid fluidized bed of Geldart B particles is modeled using CFD.

• Predictions of heterogeneous EMMS and homogenous Gidaspow drag models are compared.

• Effects of restitution and specularity coefficients are examined.

• Vertical segregation is simulated for differently sized solids in a bed.

• Polysilicon FBR is simulated using both Gidaspow and EMMS drag models.

Abstract

The energy minimization multi-scale (EMMS) is a heterogeneous drag model widely used to simulate gas–solid fluidized beds. In this work, we conducted computational fluid dynamics simulations of a gas–solid fluidized bed for Geldart B particles to compare the EMMS with the homogeneous Gidaspow drag model. The results from both the homogeneous and heterogeneous drag models were compared with literature experimental data on pressure drop and bed expansion. There was no noticeable difference in predicted bed characteristics in the slugging regime. However, in the turbulent regime, the EMMS model predicted slightly lower bed expansion than did the Gidaspow model. We evaluated the effects of solid–solid and solid–wall interaction parameters by varying the restitution and specularity coefficients. Bed expansion increases by a factor of 1.05–1.08 when the restitution coefficient increases from 0.9 to 0.99. The models predict a higher solid volume fraction and higher solid downflow velocity near the wall for a low specularity coefficient of 0.01 or 0. When we considered solid phases of different sizes to model polydisperity, the simulation predicted vertical segregation of 300, 350, and 400 μm in the fluidized region due to gravity. Furthermore, the drag models made similar predictions in bad characteristics from cold model simulation of a polysilicon fluidized-bed reactor, although there was very little vertical segregation of solid particles for this case.

Graphical abstract

Keywords

CFD simulation; Energy minimization multi-scale drag; Gas–solid fluidized bed; Polydisperity; Fluidized-bed reactor

文章导读