Influence of the rolling-resistance-based shape of coarse particles on the shear responses of granular mixtures--颗粒学报PARTICUOLOGY

Zhu, Y., Nie, Z., & Gong, J. (2020). Influence of the rolling-resistance-based shape of coarse particles on the shear responses of granular mixtures. Particuology, 52, 67-82. https://doi.org/10.1016/j.partic.2019.12.004

Influence of the rolling-resistance-based shape of coarse particles on the shear responses of granular mixtures

Yangui Zhu ^a, Zhihong Nie ^a, Jian Gong ^b *

a School of Civil Engineering, Central South University, Changsha 410075, China
b School of Hydraulic Engineering, Changsha University of Science and Technology, Changsha 410114, China

10.1016/j.partic.2019.12.004

Volume 52, October 2020, Pages 67-82

Received 19 September 2019, Revised 1 December 2019, Accepted 4 December 2019, Available online 23 January 2020, Version of Record 24 June 2020.

E-mail: gj_csu@hotmail.com

Highlights

• We study shear responses of particle mixtures with rolling friction coefficient μ_r.

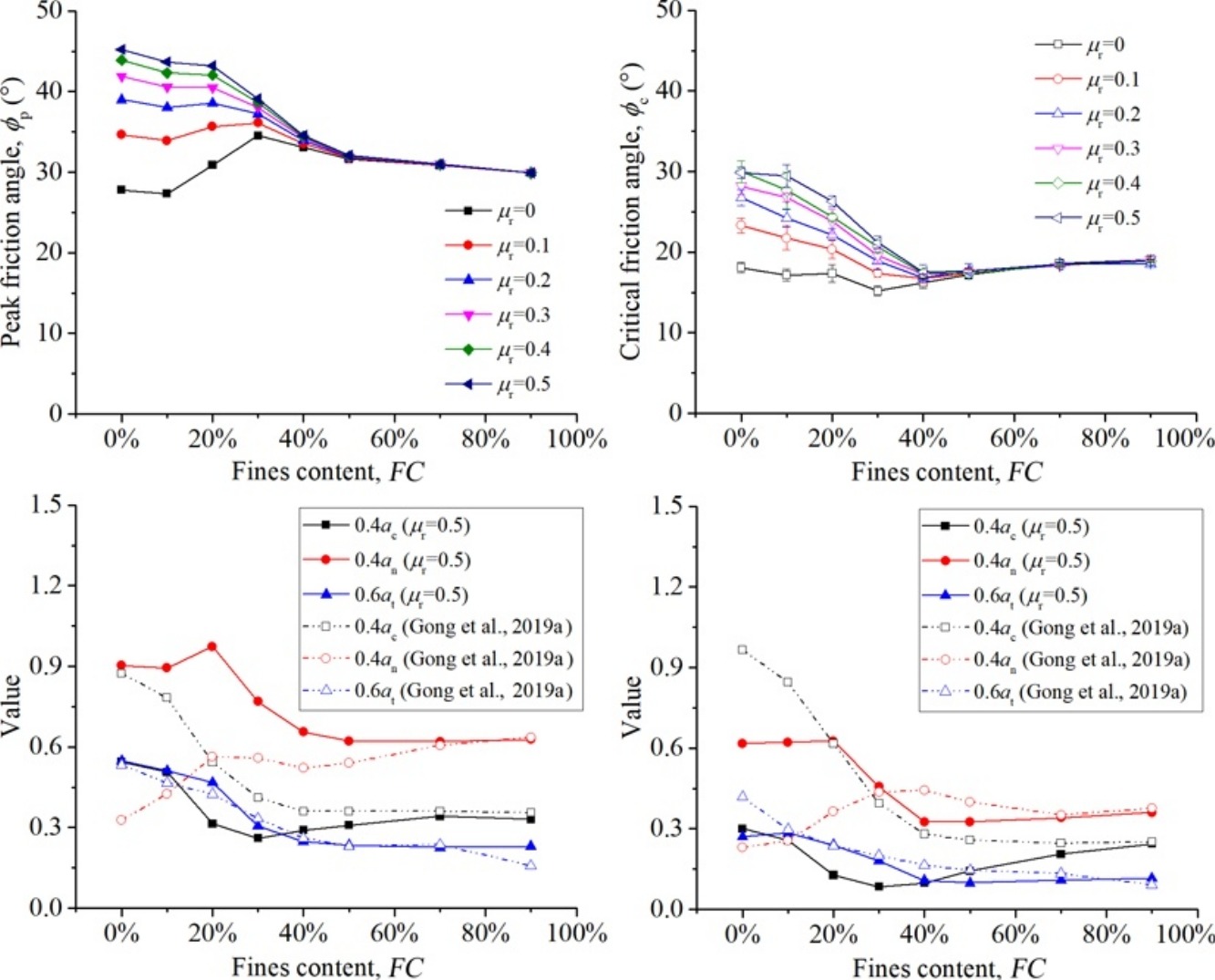
•Anisotropies reveal the variations of q/p' with μ_r and fine content (FC).

• Mixtures of coarse particles with μ_r = 0.5 and gravel particles are compared.

• Rolling resistance weakens the relationship q/p' =ka_c^sn when FC = 30% and 40%.

Abstract

Shear responses of dense granular mixtures of spherical coarse particles with the rolling resistance and spherical fine particles are studied via triaxial compression tests using the discrete element method. The macroscale responses (shear strength and dilatancy) are examined. Comparing the results with those in the literature indicates that granular mixtures with a rolling resistance coefficient of 0.5 have similar macroscale responses to those of gravel-shaped coarse particle mixtures. We quantify the microscale responses including the percentage contributions of contact types, partial coordination number, average particle rotation, average degree of interlocking, and local structural properties. A detailed analysis of the force–fabric anisotropy reveals the mechanisms of the variations in the shear strength with the rolling resistance coefficient and the fines content. The mechanism of the variation in the shear strength with the fines content for granular mixtures with a rolling resistance coefficient of 0.5 is different from that for gravel-shaped coarse particle mixtures. Finally, we find that a rolling resistance linear model weakens the linear relationship between the stress ratio and the fabric anisotropy of strong and non-sliding contacts when the fines content is 30% and 40%.

Graphical abstract

Keywords

Granular mixture; Rolling resistance; Particle shape; Fines content; Macroscale and microscale responses; Anisotropy

文章导读