Dynamic flowsheet simulation of re-entrainment from particle layers formed inside electrostatic precipitators--颗粒学报PARTICUOLOGY

Sander, S., & Fritsching, U. (2020). Dynamic flowsheet simulation of re-entrainment from particle layers formed inside electrostatic precipitators. Particuology, 53, 41-47. https://doi.org/10.1016/j.partic.2019.12.009

Dynamic flowsheet simulation of re-entrainment from particle layers formed inside electrostatic precipitators

Sören Sander ^a *, Udo Fritsching ^{a b}

a Particles and Process Engineering, University of Bremen, Bibliothekstrasse 1, 28359 Bremen, Germany
b Process Engineering, Leibniz-Institut für Werkstofforientierte Technologien – IWT, Badgasteiner Strasse 3, 28359 Bremen, Germany

10.1016/j.partic.2019.12.009

Volume 53, December 2020, Pages 41-47

Received 29 September 2019, Accepted 13 December 2019, Available online 20 February 2020, Version of Record 16 December 2020.

E-mail: sander@iwt.uni-bremen.de

Highlights

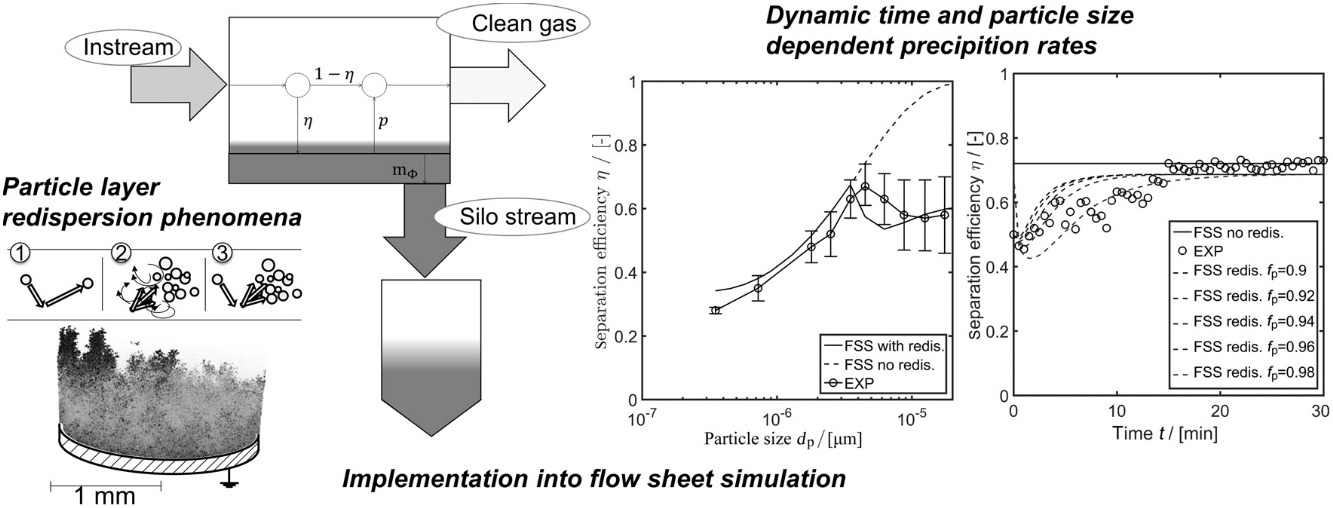
• Macroscopic simulation of an electrostatic precipitator.

• Particle charging and transport have density and permittivity effects.

• These effects affect the precipitation of submicron- and micron-sized particles.

• The effect of redispersion effects on separation efficiency is discussed.

Abstract

Electrostatic precipitators clean away the particulate matter of exhaust gases in manifold industrial processes. Parameter studies of particle separation in the size range of several 100 nm to 25 μm is of particular interest for the prediction of precipitation efficiencies and emissions. Models typically cover the transport of particles towards walls of the precipitator. However, no model yet covers the possible re-entrainment of particles from layers formed at the walls back into the gas flow. This study presents the implementation of a new time-resolving model for electrostatic precipitation utilizing a re-entrainment model. Experimental data support the results of modelling. The model uses a statistical approach based on properties of the particulate layer forming at the precipitator walls. The model is used for the analysis of the redispersion of particles in a laboratory-scale electrostatic precipitator (Sander, Gawor, & Fritsching, 2018). Results show reduced precipitation efficiencies for particles larger than 5 μm as particles have higher kinetic impact energies and lower bounding energy at the layer surface. Time dynamics reveal a steady-state behavior of the separation for CaCO₃ (limestone, trademark "Ulmer Weiss®") while Al₂O₃ (trademark "Pural NF®") precipitation is affected by layer buildup at the walls increasing over several minutes.

Graphical abstract

Keywords

Electrostatic precipitator; Flow sheet model; Redispersion and re-entrainment; Gas cleaning; Particle layer

文章导读