Resuspension of spherical particles due to surface vibration--颗粒学报PARTICUOLOGY

Chatoutsidou, S. E., & Lazaridis, M. (2021). Resuspension of spherical particles due to surface vibration. Particuology, 54, 126-135. https://doi.org/10.1016/j.partic.2020.08.003

Resuspension of spherical particles due to surface vibration

Sofia Eirini Chatoutsidou ^*, Mihalis Lazaridis

School of Environmental Engineering, Technical University of Crete, 73100 Chania, Greece

10.1016/j.partic.2020.08.003

Volume 54, February 2021, Pages 126-135

Received 9 October 2018, Revised 25 February 2020, Accepted 26 August 2020, Available online 23 September 2020, Version of Record 28 January 2021.

E-mail: sochatoutsidou@isc.tuc.gr

Highlights

• Particle resuspension due to surface vibration was investigated.

• An external vibrating force was considered to apply normal on a thin plate.

• Oscillations in the vertical direction were propagated through bending waves.

• Particle motion was initiated provided that inertia due to its mass was overcome.

• A force balance method was used to investigate whether particle resuspension occurred.

Abstract

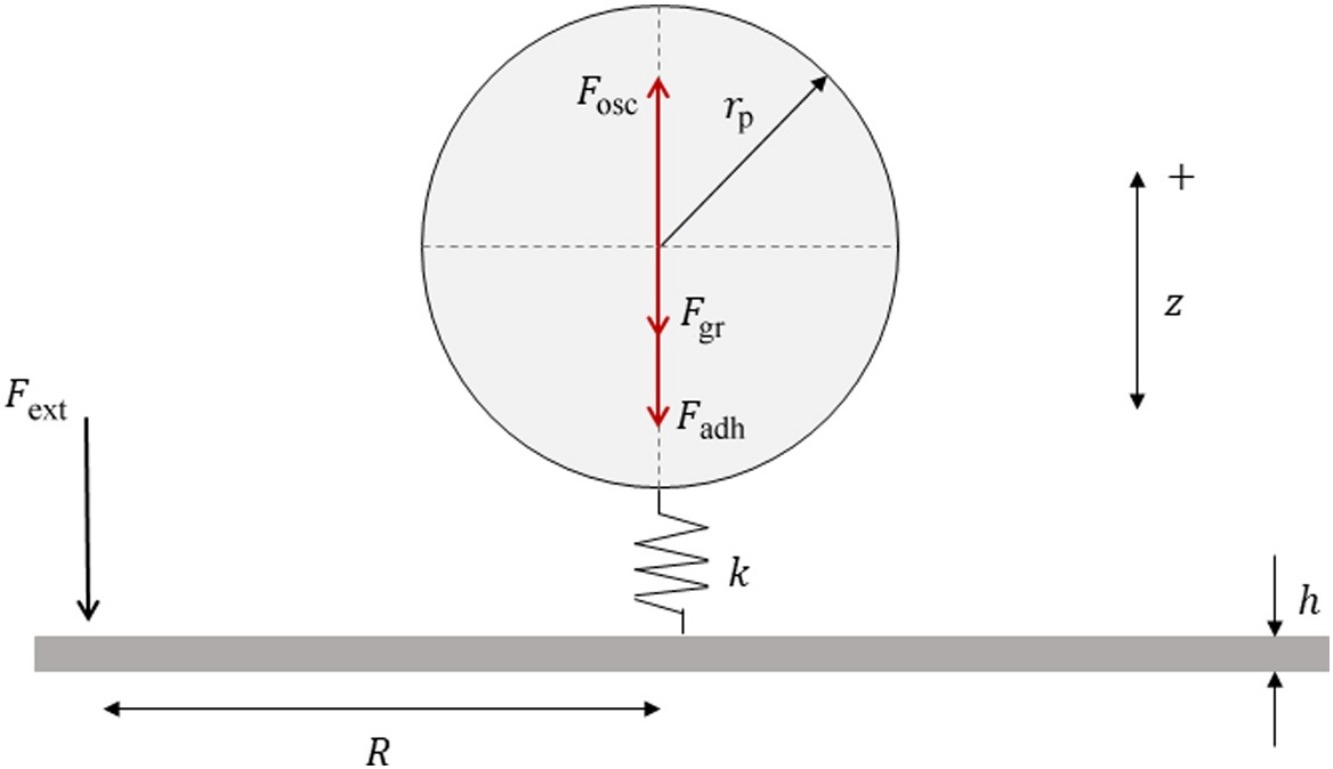
In this study, particle resuspension due to surface vibration was investigated. A spherical particle was assumed to rest on top of a thin plate, and an external vibrating force was applied normal on the plate at t = 0 and at distance R from the particle. The external driving force created a displacement field in both time and space domains, where deformations in the body of the plate were considered small elastic oscillations that are perpendicular to the propagation of the displacement. Free oscillations were introduced via the theory of elasticity and the creation of waves on thin plates, i.e., bending waves. Particle motion in the vertical direction was initiated through plate displacement, provided that inertia due to particle mass is overcome. In particular, the particle was assumed to oscillate with a force (of oscillation) estimated via Newton’s second law of motion, comprising of two components: the acceleration due to the plate displacement and the particle mass. Subsequently, a simple force balance method was used to determine the conditions for resuspension. Accordingly, resuspension occurs when the oscillation force exceeds the couple of the adhesive and gravitational forces. The results suggest that the plate displacement depends on the characteristics of the applied force, material properties, and plate thickness. In addition, it was found that the oscillation force is substantially lower than the applied force and that it depends on plate displacement and particle mass. Additionally, the particle size significantly influencedthe outcome of resuspension. Thus, resuspension is favorable for large particles, strong applied forces, and high forcing frequencies.

Graphical abstract

Keywords

Particle resuspension; Vibration; Bending waves

文章导读