Flow characteristics of nonspherical granular materials simulated with multi-superquadric elements--颗粒学报PARTICUOLOGY

Wang, S., & Ji, S. (2021). Flow characteristics of nonspherical granular materials simulated with multi-superquadric elements. Particuology, 54, 25-36. https://doi.org/10.1016/j.partic.2020.04.002

Flow characteristics of nonspherical granular materials simulated with multi-superquadric elements

Siqiang Wang, Shunying Ji ^*

State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023, China

10.1016/j.partic.2020.04.002

Volume 54, February 2021, Pages 25-36

Received 16 January 2020, Revised 30 March 2020, Accepted 15 April 2020, Available online 1 June 2020, Version of Record 28 January 2021.

E-mail: jisy@dlut.edu.cn

Highlights

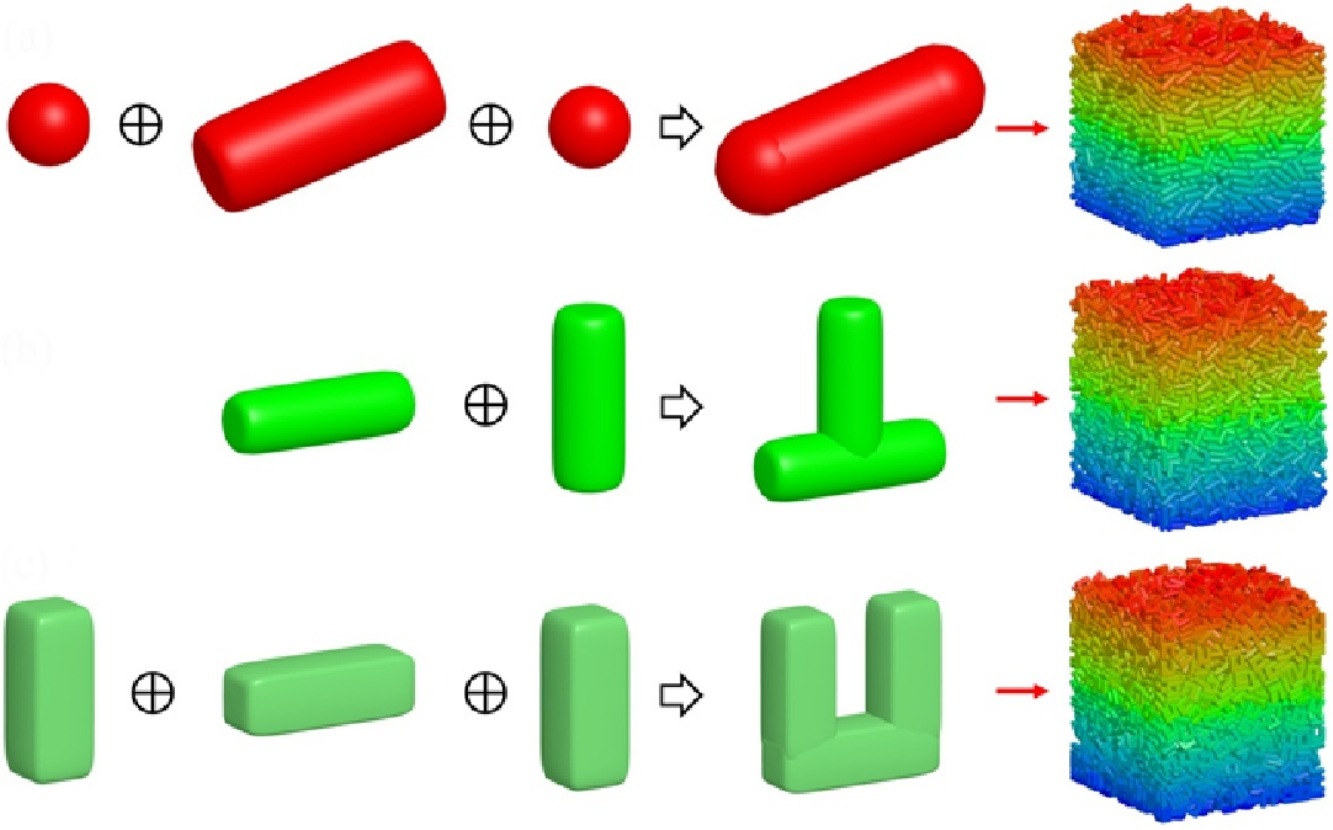
• A multi-superquadric method is developed using a superquadric equation.

• Concave particles are constructed with the multi-superquadric method.

• Flow characteristics of concave and convex particles are compared using the DEM.

Abstract

The superquadric equation is typically used to mathematically describe nonspherical particles and construct particle shapes with different surface sharpness and aspect ratios. However, nonspherical elements constructed using the superquadric equation are strictly convex, limiting their engineering application. In this study, a multi-superquadric model based on a superquadric equation is developed. The model combines several superquadric elements that can be used to construct concave and convex particle shapes. Four tests are performed to examine the applicability of the multi-superquadric approach. The first involves a comparison of theoretical results for a single spherocylinder impacting a flat wall. The second involves the formation of a nonspherical granular bed. The third investigates the effects of the particle shape on the hopper discharge and angle of repose. The final test evaluates the mixing behaviors of granular materials within a horizontally rotating drum. These tests demonstrate the applicability of the multi-superquadric approach to nonspherical granular systems. Furthermore, the effects of particle shape on the packing density, discharge rate, angle of repose, and Lacey mixing index are discussed. Results indicate that concave particles have a lower packing density, flow rate, and mixing rate and higher angles of repose than convex particles. Interlocking of elements becomes more pronounced for concave particles and results in local cluster structures, thereby enhancing the stability of granular systems and limiting sliding or rotation between nonspherical particles.

Graphical abstract

Keywords

Multi-superquadric approach; Nonspherical elements; Concave particles; Discrete element method; Granular materials

文章导读