Computation of pressure drop for dilute gas–solid suspension across thin and thick orifices--颗粒学报PARTICUOLOGY

Senapati, S. K., & Dash, S. K. (2021). Computation of pressure drop for dilute gas–solid suspension across thin and thick orifices. Particuology, 55, 209-221. https://doi.org/10.1016/j.partic.2020.07.003

Computation of pressure drop for dilute gas–solid suspension across thin and thick orifices

Santosh Kumar Senapati ^*, Sukanta Kumar Dash

Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, West Bengal 721302, India

10.1016/j.partic.2020.07.003

Volume 55, April 2021, Pages 209-221

Received 26 June 2019, Revised 4 June 2020, Accepted 7 July 2020, Available online 7 August 2020, Version of Record 3 February 2021.

E-mail: senapatis431@gmail.com; sks90@iitkgp.ac.in

Highlights

• Gas–solid flow pressure drop was computed across thin and thick orifices.

• Combined effects of collisions and pertinent parameters on pressure drop were determined.

• Thick orifices result in higher pressure drop than the thinner ones.

• Orifice thickness is prominent at high Reynolds number and solid loading.

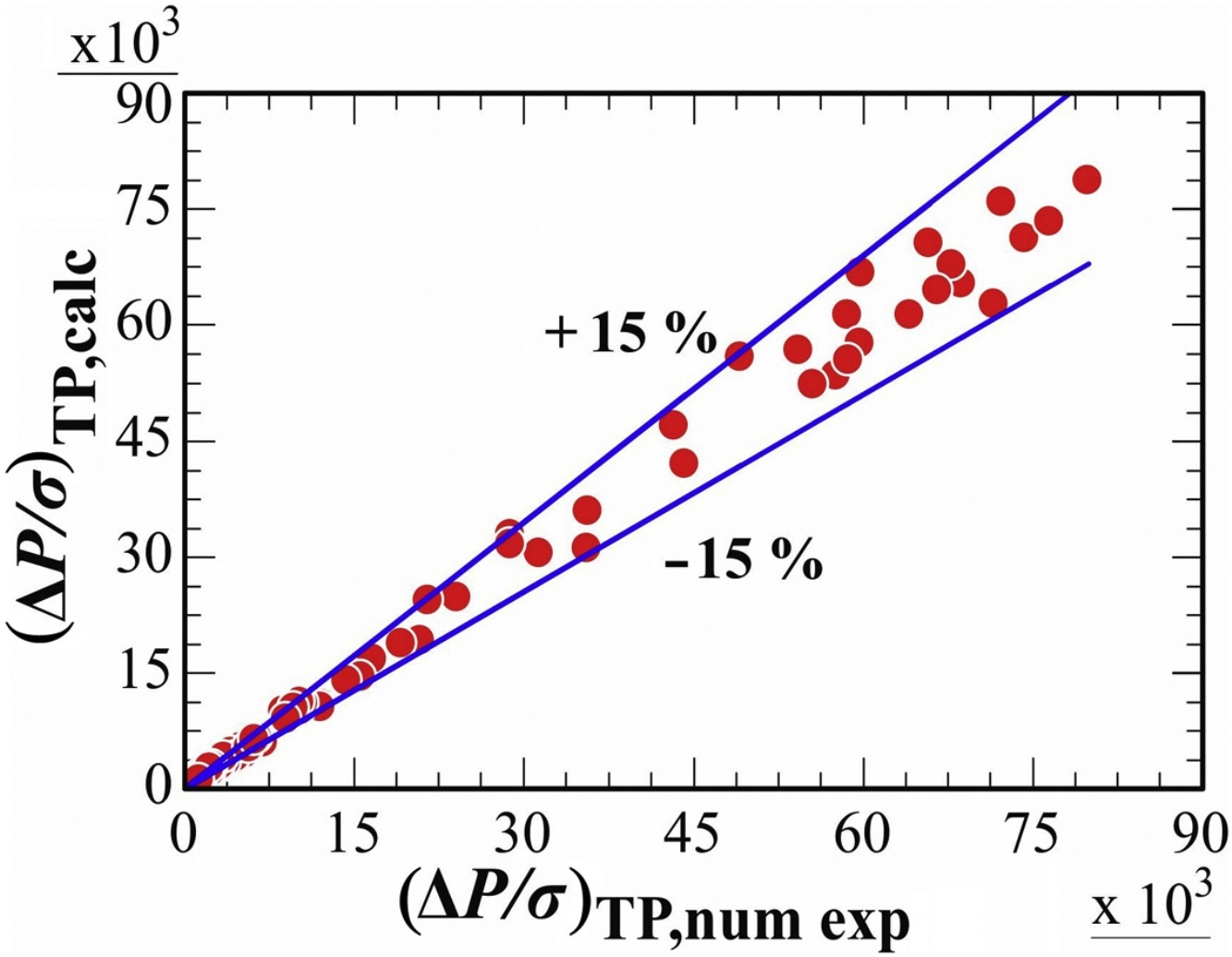
• Two-phase multiplier was proposed for the pressure drop with accuracy within 15%.

Abstract

The present work deals with the computation of the gas–solid two-phase flow pressure drop across thin and thick orifices for a vertically downward flow configuration at the higher limits of a dilute phase flow situation 0.01 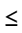$≤$ α_s, in 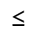$\, ≤$ 0.10. The Eulerian–Eulerian (two-fluid) model has been used in conjunction with the kinetic theory of granular flow with a four-way coupling approach. The validation of the solution process has been performed by comparing the computational result with the existing experimental data. It is observed that the two-phase flow pressure drop across the orifice increases with an increase in the thickness of the orifice, and the effect is more prominent at higher solid loading. The pressure drop is found to increase with an increase in the solid volume fraction. An increase in the Reynolds number or the area ratio increases the pressure drop. An increase in the size of the particles reduces the pressure drop across the orifice at both small and relatively large solid volume fractions. Finally, a two-phase multiplier has been proposed in terms of the relevant parameters, which can be useful to evaluate the gas–solid two-phase flow pressure drop across the orifice and can subsequently help to improve the system performance.

Graphical abstract

Keywords

Dilute phase flow; Gas-solid flow; Thin and thick orifice; Vertically downward flow; Pressure drop

文章导读