Influence of the pressure drop and the air lock on the solid flux in a cross-flow moving bed--颗粒学报PARTICUOLOGY

Wang, R., Wang, D., Fan, Y., & Lu, C. (2021). Influence of the pressure drop and the air lock on the solid flux in a cross-flow moving bed. Particuology, 55, 166-178. https://doi.org/10.1016/j.partic.2020.06.006

Influence of the pressure drop and the air lock on the solid flux in a cross-flow moving bed

Ruojin Wang ^{a b}, Dewu Wang ^a, Yiping Fan ^b *, Chunxi Lu ^b *

a School of Chemical Engineering and Technology, Hebei University of Technology, Tianjin 300130, China
b College of Chemical Engineering, State Key Laboratory of Heavy Oil Processing, China University of Petroleum, Beijing 102249, China

10.1016/j.partic.2020.06.006

Volume 55, April 2021, Pages 166-178

Received 16 January 2020, Revised 8 April 2020, Accepted 29 June 2020, Available online 26 July 2020, Version of Record 3 February 2021.

E-mail: fanyipin2002@sina.com; lcx725@sina.com

Highlights

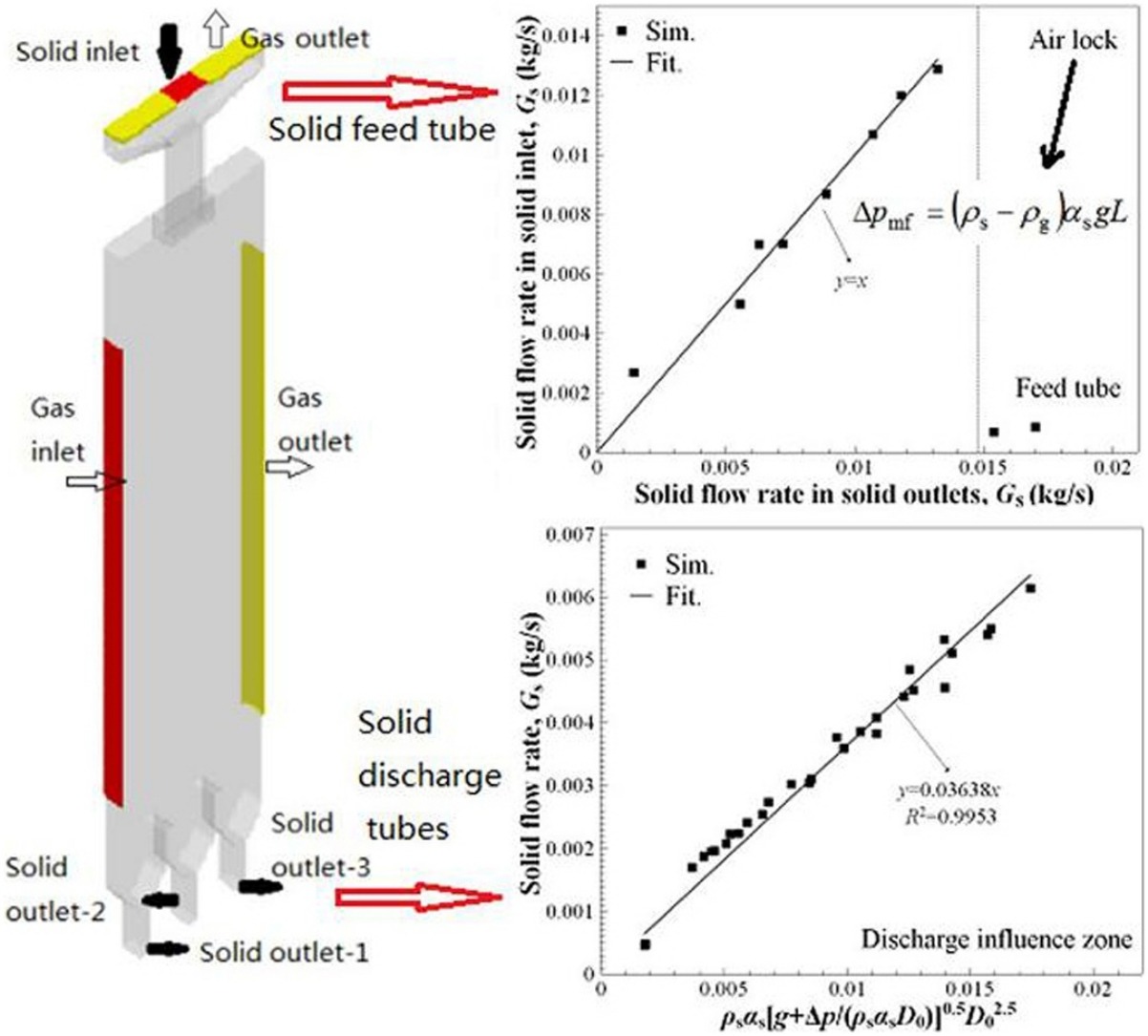
• Gas–solid flow pattern is well simulated by the Barracuda software.

• Pressure drop in the solid feed/discharge tubes are computed by proposed methods.

• Gas frictional/local resistances dominate pressure drop in solid feed/discharge tubes.

• Solid flux equation is given considering both pressure drop and air lock factors.

Abstract

The gas–solid flow pattern in a rectangular cross-flow moving bed is simulated by the multiphase particle-in-cell (MP-PIC) model with the Barracuda software. The computed results are verified by the experimental data. In the bed, the actual solid flux generally equals the solid flow rates in the solid feed and discharge tubes. However, these two flow rates are greatly influenced by the air lock and the pressure drop in the solid feed and discharge tubes, namely, the negative and positive pressure gradients, respectively, rather than the traditional opinion that they are merely controlled by the valve openings. The pressure drops in these tubes are calculated by the proposed “common pressure pool with multiple outlets” (CPPMO) and the “common pressure pool” (CPP) methods. It is found that the local gas resistance dominates the pressure drop in the solid discharge tubes, while the gas frictional resistance determines the pressure drop in the solid feed tube. In addition, when the solid flow rate nearly tends to zero in the solid feed tube, the air lock forms. A solid flux equation is then given by considering both the air lock and the pressure drop factors in the cross-flow moving bed.

Graphical abstract

Keywords

Cross-flow moving bed; Barracuda; Solid flux; Pressure drop; Air lock

文章导读