Computational fluid dynamic–discrete element method coupling analysis of particle transport in branched networks--颗粒学报PARTICUOLOGY

Wang, X., Yao, J., Gong, L., Li, Y., Yang, Y., & Zhao, H. (2021). Computational fluid dynamic–discrete element method coupling analysis of particle transport in branched networks. Particuology, 55, 140-150. https://doi.org/10.1016/j.partic.2020.05.005

Computational fluid dynamic–discrete element method coupling analysis of particle transport in branched networks

Xiaoyu Wang ^a, Jun Yao ^a, Liang Gong ^{a b *}, Yang Li ^{a c *}, Yongfei Yang ^a, Hongliang Zhao ^d

a Research Center of Multiphase Flow in Porous Media, China University of Petroleum (East China), Qingdao 266580, China
b College of New Energy, China University of Petroleum (East China), Qingdao 266580, China
c Department of Oilfield Exploration & Development, Sinopec, Beijing 100029, China
d School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China

10.1016/j.partic.2020.05.005

Volume 55, April 2021, Pages 140-150

Received 26 February 2020, Revised 14 May 2020, Accepted 19 May 2020, Available online 23 June 2020, Version of Record 3 February 2021.

E-mail: lgong@upc.edu.cn; rcogfr_upc@126.com

Highlights

• Particle transport characteristics in branched network were analyzed quantitatively.

• Geometric features of branched networks influenced particle shunting.

• Injection position determined future flow path of particles in the networks.

• Joint influence of inertial, shunt capacity and upstream flow was investigated.

Abstract

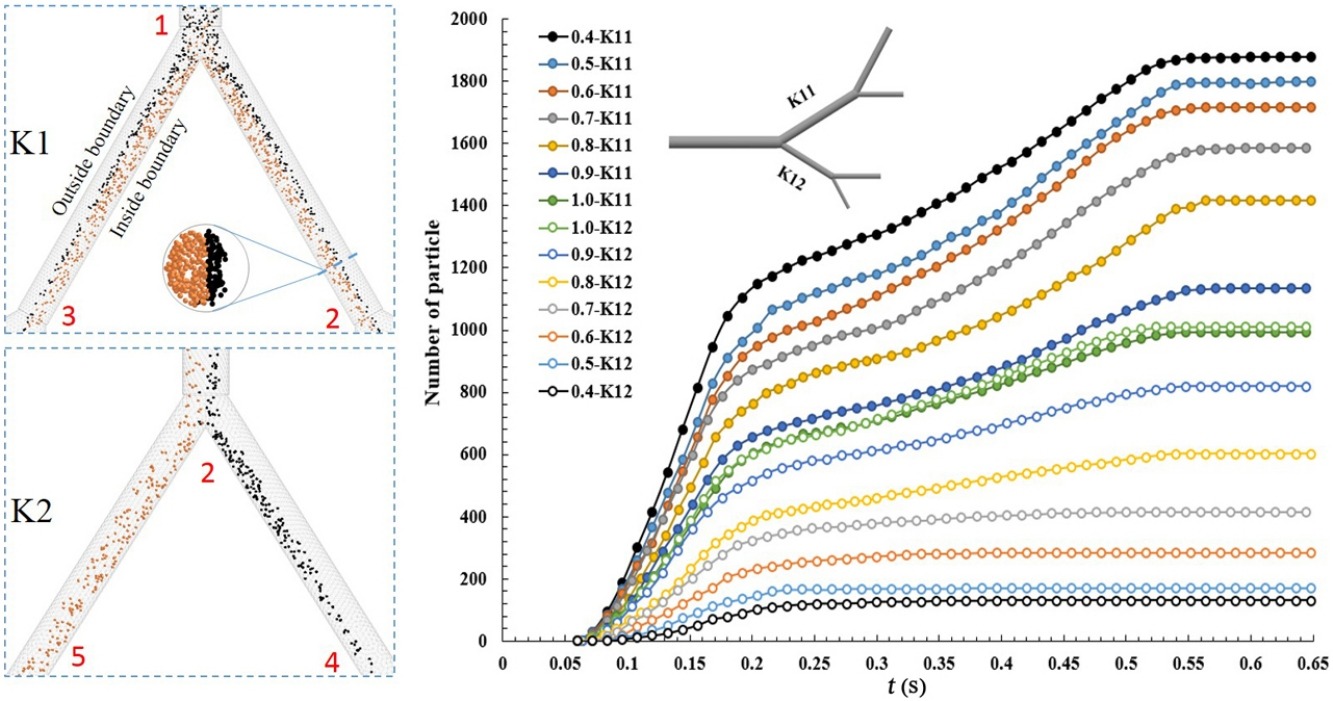
An understanding of the particle transport characteristics in a branched network helps to predict the particle distribution and prevent undesired plugging in various engineering systems. Quantitative analysis of particle flow characteristics is challenging in that experiments are expensive and particle flow is difficult to detect without disturbing the flow. To overcome this difficulty, man-made fractal tree-like branched networks were built, and a coupled computational fluid dynamic and discrete element method model was applied. A series of numerical simulations was carried out to analyze the influence of fractal structure parameters of networks on the particle flow characteristics. The joint influence of inertial, shunt capacity and superposition from upstream branches on particle flow was investigated. The injection position at the inlet determined the particle velocity and its future flow path. The particle density ratio, particle size and bifurcation angle had a greater influence on the shunting of K2 branches than that in the K1 level and Nk22/Nk21 reached a maximum at 60°. Compared with a network with an even number of branches, there was a preferential branch when the branch number was odd. The preferential branch effect or asymmetry degree of the level (K2) branches had a more significant impact on particle shunting than that from the upstream branches (K1).

Graphical abstract

Keywords

Particle-fluid flow; CFD-DEM coupling; Branched network

文章导读