Effect of particle type on the shear behaviour of granular materials--颗粒学报PARTICUOLOGY

Liu, S., Nie, Z., Hu, W., Gong, J., & Lei, P. (2021). Effect of particle type on the shear behaviour of granular materials. Particuology, 56, 124-131. https://doi.org/10.1016/j.partic.2020.11.001

Effect of particle type on the shear behaviour of granular materials

Shunkai Liu ^a, Zhihong Nie ^a, Wei Hu ^b *, Jian Gong ^a, Peng Lei ^c

a School of Civil Engineering, Central South University, Changsha 410075, China
b Hunan Province Key Laboratory of Geotechnical Engineering Stability Control and Health Monitoring, Hunan University of Science and Technology, Xiangtan 411201, China
c School of Hydraulic Engineering, Changsha University of Science and Technology, Changsha 410114, China

10.1016/j.partic.2020.11.001

Volume 56, June 2021, Pages 124-131

Received 18 June 2020, Revised 31 October 2020, Accepted 10 November 2020, Available online 23 November 2020, Version of Record 8 March 2021.

E-mail: yilukuangben@hnust.edu.cn

Highlights

• The effect of convex true and multi-sphere ellipsoids on shear strength was studied.

• The effects of the two particle types on fabric anisotropy were compared.

• The different shear strength was explained in terms of micromechanics.

Abstract

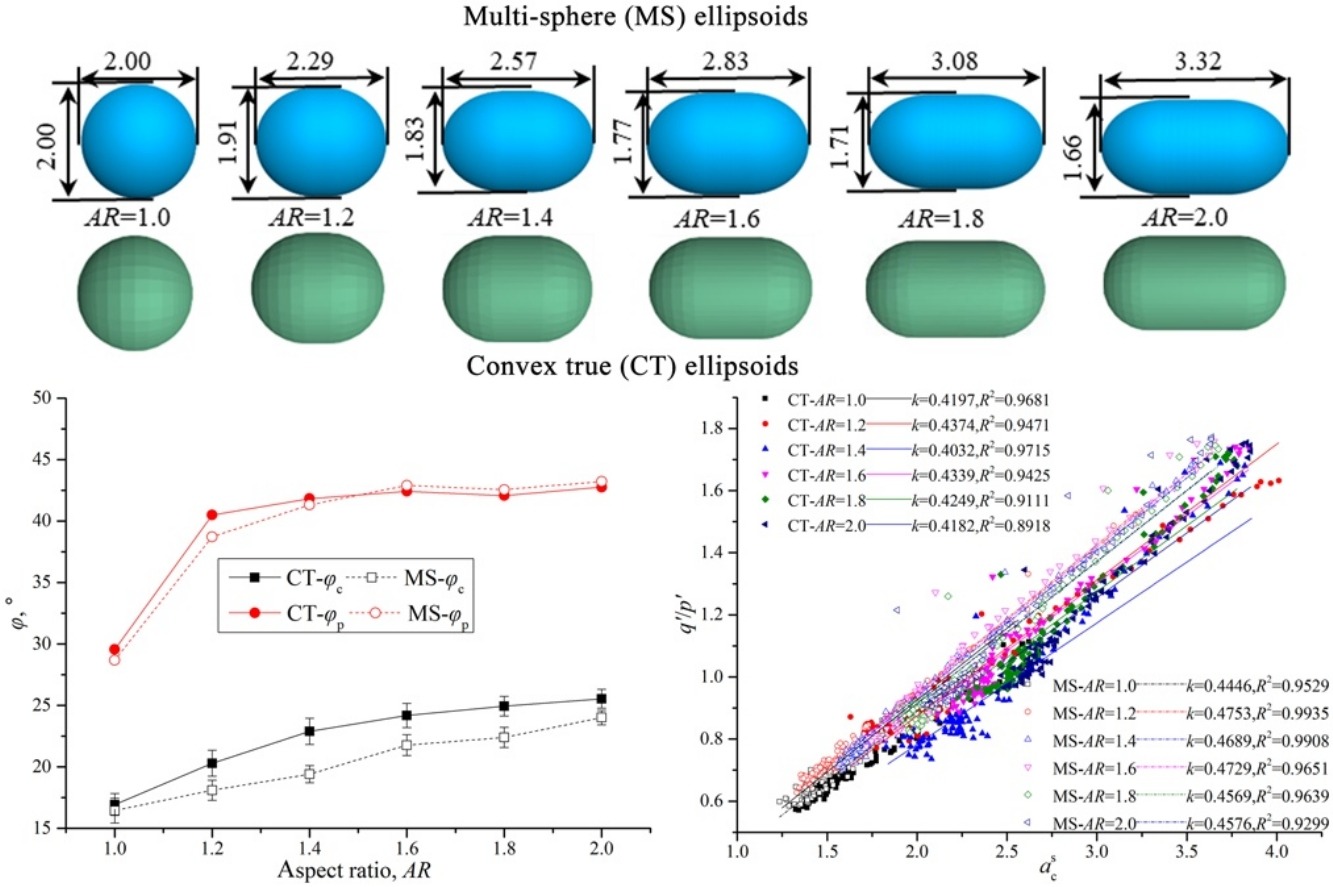
In discrete element method (DEM) simulations, multi-sphere (MS) clumped and convex particles are two main particle models that are used to study the mechanical behaviours of granular materials. Of interest is the evaluation of the effect of multiple contacts between clumped particles or single contacts between convex particles on the mechanical behaviours of granular materials. In this context, a series of drained triaxial compression tests were conducted on convex true (CT) ellipsoids and MS ellipsoids with aspect ratios (ARs) ranging from 1.0–2.0. The microscale results indicate that at a given AR, the critical friction angle φc changes with the particle type, whereas the peak friction angle φp is nearly independent of the particle type. The anisotropic analysis provides underlying mechanisms of the shear strength evolution from two perspectives. First, the anisotropies of granular materials are essential to shear strength as the deviatoric (q)-to-effective mean (p′) stress ratio can be expressed as the sum of the anisotropies, i.e., q/q' ≈ 0.4 a_c + 0.4 a_n + 0.6 a_t_{$q / p^{'} \approx 0 .4 a_{c} + 0 .4 a_{n} + 0 .6 a_{t}$}, where ac, an and at are the normal contact anisotropy, normal contact force anisotropy and tangential contact force anisotropy, respectively. For all samples, ac and an underpin the shear strength and are influenced by the particle type. The similar φp displayed by the CT and MS ellipsoids does not translate to similar an and ac but similar ac+an for the two particle types. In addition, owing to their larger ac+an, the CT ellipsoids have a higher φc than the MS ellipsoids. Second, there is a satisfactory linear relationship between $q / p^{'}$ q/p′ and ac within strong and non-sliding (sn) contacts $a_{c}^{sn}$ a_c^sn(i.e., _q/p′ = k $k a_{c}^{sn}$ a_c^sn), where k is the fitting parameter. Accordingly, in the peak state, the subtle difference in shear strength is attributed to the greater $a_{c}^{sn}$ in the CT ellipsoids than in the MS ellipsoids that is counteracted by the smaller k. However, in the critical state, the greater difference in a_c^sn between the CT and MS ellipsoids is partially offset by the smaller difference in k, causing a higher φc in the CT ellipsoids than in the MS ellipsoids.

Graphical abstract

Keywords

Multi-sphere clump; Convex true particle; DEM; Particle type; Anisotropy; Shear strength

文章导读