An assessment of steady-state conditions in single slug horizontal pneumatic conveying--颗粒学报PARTICUOLOGY

Lavrinec, A., Orozovic, O., Rajabnia, H., Williams, K., Jones, M. G., & Klinzing, G. E. (2021). An assessment of steady-state conditions in single slug horizontal pneumatic conveying. Particuology, 58, 187-195. https://doi.org/10.1016/j.partic.2021.04.007

An assessment of steady-state conditions in single slug horizontal pneumatic conveying

A. Lavrinec ^a *, O. Orozovic ^a, H. Rajabnia ^a, K. Williams ^a, M.G. Jones ^a, G.E. Klinzing ^b

a Centre for Bulk Solids and Particulate Technologies, The University of Newcastle, NSW 2308, Australia
b Department of Chemical and Petroleum Engineering, The University of Pittsburgh, PA 15261, USA

10.1016/j.partic.2021.04.007

Volume 58, October 2021, Pages 187-195

Received 30 October 2020, Revised 4 April 2021, Accepted 14 April 2021, Available online 4 May 2021, Version of Record 13 September 2021.

E-mail: aleksej.lavrinec@uon.edu.au

Highlights

• CFD–DEM used to study dense phase pneumatic conveying.

• Inlet velocity, layer height and initial lengths systematically varied.

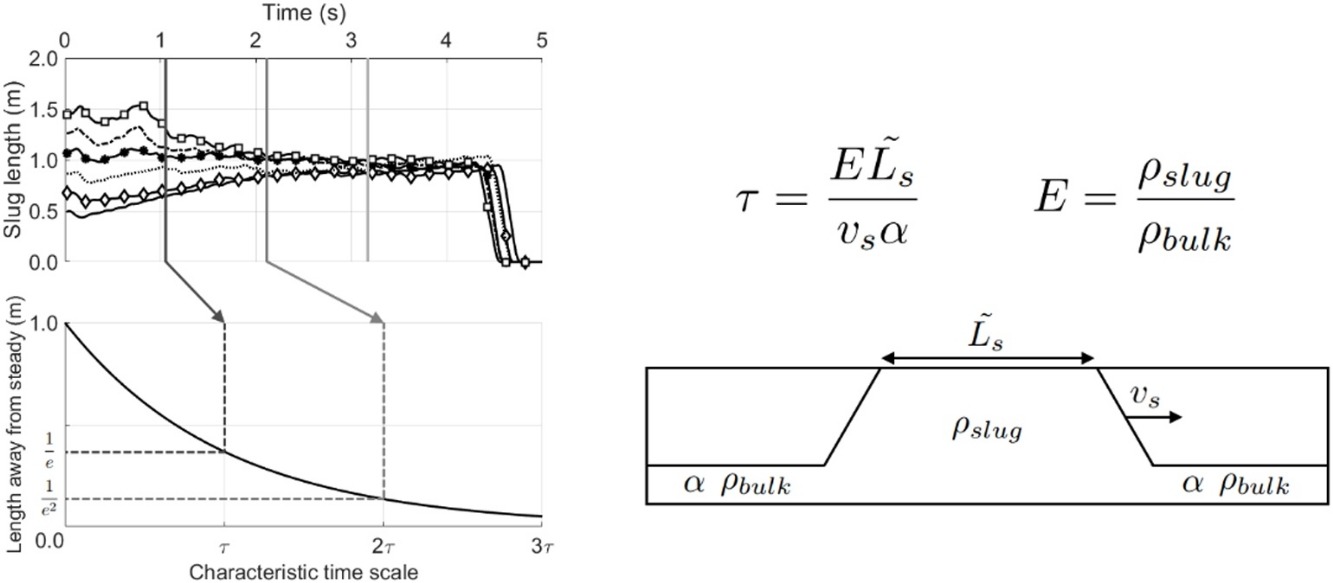
• Theoretical derivation shows how slugs tend to steady state.

• Characteristic time devised that can estimate how fast slugs tend to steady state.

• Steady length, velocity and porosity depend on layer height and inlet velocity.

Abstract

This study used a 3D coupled CFD–DEM model to assess how slugs tend towards steady state in single slug horizontal pneumatic conveying. Initial slug length, inlet velocity and initial stationary layer fractions were systematically varied for a total of 72 simulations. Previously made observation that slugs tend towards a steady state was confirmed via a theoretical derivation. The derivation shows that slugs move towards their steady state lengths exponentially. This allowed for a calculation of a characteristic time scale which is a measure of how quickly a slug tends towards the steady state. The theoretical estimate which is a function of slug porosity, steady length, velocity and stationary layer fraction has good agreement with simulated results. A link between steady slug length and solids loading ratio was also shown.

Graphical abstract

Keywords

Pneumatic conveying; Dense phase; Slug flow; Steady state

文章导读