Numerical simulation of the drag and heat-transfer characteristics around and through a porous particle based on the lattice Boltzmann method--颗粒学报PARTICUOLOGY

Zhang, M., Zhao, Q., Huang, Z., Chen, L., & Jin, H. (2021). Numerical simulation of the drag and heat-transfer characteristics around and through a porous particle based on the lattice Boltzmann method. Particuology, 58, 99-107. https://doi.org/10.1016/j.partic.2021.01.013

Numerical simulation of the drag and heat-transfer characteristics around and through a porous particle based on the lattice Boltzmann method

Mingyue Zhang, Qiuyang Zhao, Zujie Huang, Lei Chen, Hui Jin ^*

State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China

10.1016/j.partic.2021.01.013

Volume 58, October 2021, Pages 99-107

Received 1 January 2021, Revised 21 January 2021, Accepted 21 January 2021, Available online 18 March 2021, Version of Record 27 March 2021.

E-mail: jinhui@mail.xjtu.edu.cn

Highlights

• Effects of the Reynolds number and Darcy number investigated.

• Lattice Boltzmann method used to solve generalized macroscopic governing equations.

• Correlations for drag coefficient and surface-averaged Nusselt number established.

Abstract

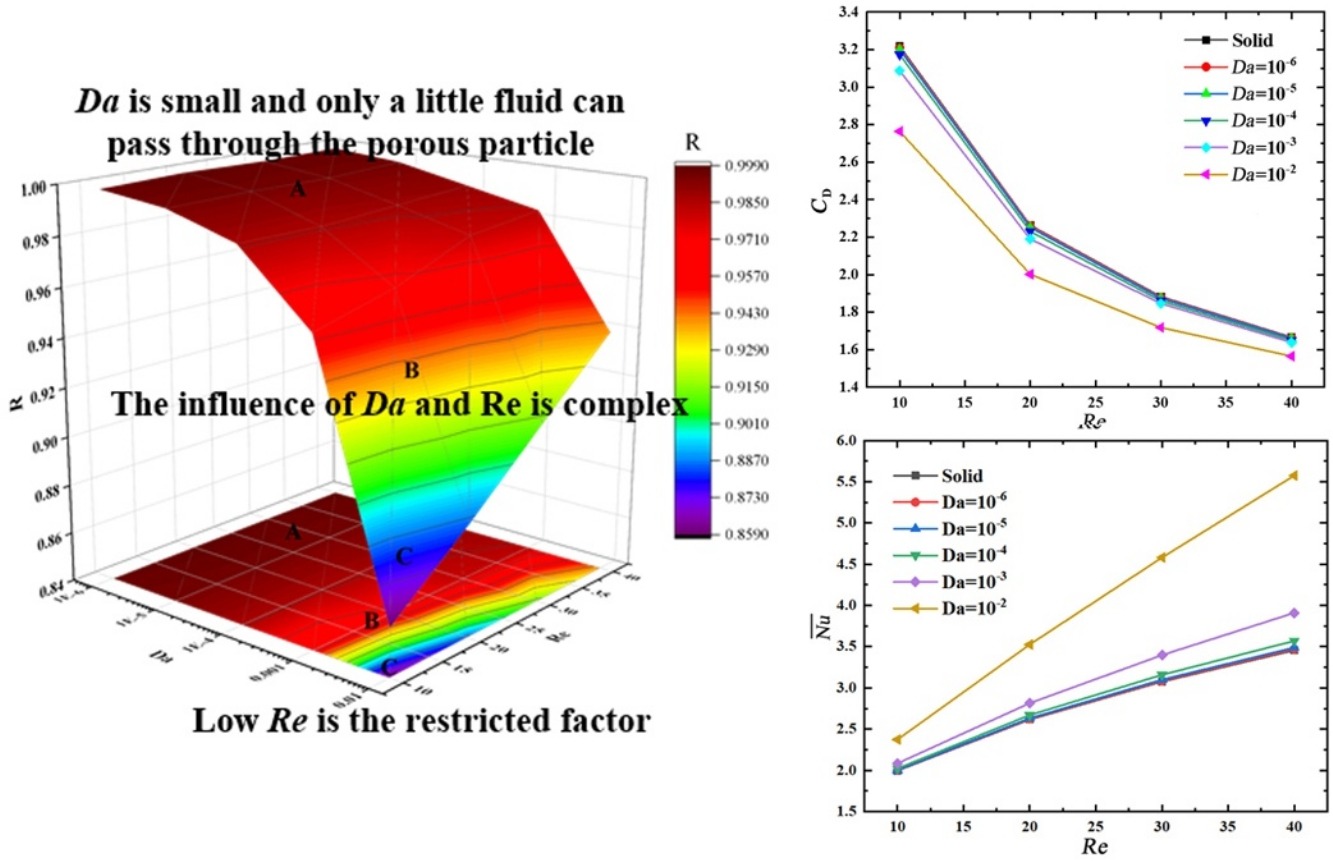
Porous particle flow is universal in nature and industry. However, in previous numerical simulations, porous particles have usually been assumed to be solid. It is necessary to study the flow and heat-transfer characteristics around porous particles because they are greatly different from those of impermeable particles. In this study, two-dimensional steady flow and heat transfer around and through a porous particle with a constant temperature placed in a cold fluid were numerically investigated. The effects of the Reynolds number (Re) and Darcy number (Da) on the flow and heat-transfer characteristics were investigated in detail. The investigated ranges of the parameters were 10 ≤ Re ≤ 40 and 10⁻⁶ ≤ Da ≤ 10⁻². It is sophisticated to simulate porous particles with traditional simulation methods because of their complicated structure. Therefore, the lattice Boltzmann method was used to solve the generalized macroscopic governing equations because of its simplicity. The drag coefficient decreased with increasing Re or Da, but the decrease was not prominent in the range 10⁻⁶ ≤ Da ≤ 10⁻⁴. The heat-transfer efficiency of the front surface was much stronger than that of the rear surface. The heat-transfer efficiency between the particle and the fluid increased with increasing Re or Da. However, for 10⁻⁶ ≤ Da ≤ 10⁻⁴, the increase was not prominent and the heat-transfer enhancement ratio was slightly larger than one. Furthermore, the effect of Da became more prominent at larger Re. In addition, new correlations for the drag coefficient and surface-averaged Nusselt number were obtained based on the simulated results.

Graphical abstract

Keywords

Porous particle; Darcy–Brinkman–Forchheimer model; Flow and heat-transfer characteristics; Lattice Boltzmann method; Correlation

文章导读