Calibration of discrete element modeling: Scaling laws and dimensionless analysis--颗粒学报PARTICUOLOGY

Wang, Y., Mora, P., & Liang, Y. (2022). Calibration of discrete element modeling: Scaling laws and dimensionless analysis. Particuology, 62, 55-62. https://doi.org/10.1016/j.partic.2021.03.020

Calibration of discrete element modeling: Scaling laws and dimensionless analysis

Yucang Wang ^a, Peter Mora ^b, Yunpei Liang ^a *

a State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China
b College of Petroleum Engineering and Geosciences, King Fahd University of Petroleum and Minerals, Saudi Arabia

10.1016/j.partic.2021.03.020

Volume 62, March 2022, Pages 55-62

Received 24 December 2020, Revised 8 March 2021, Accepted 31 March 2021, Available online 4 May 2021, Version of Record 20 September 2021.

E-mail: liangyunpei@cqu.edu.cn

Highlights

• Dynamic similarity conditions are derived for discrete element simulations.

• The scalability of linear and non-linear contact laws are also investigated.

• An example is presented to show how to calibrate the model.

• Any attempt to reduce computer time by changing sizes, stiffnesses or masses may be in vain theoretically.

Abstract

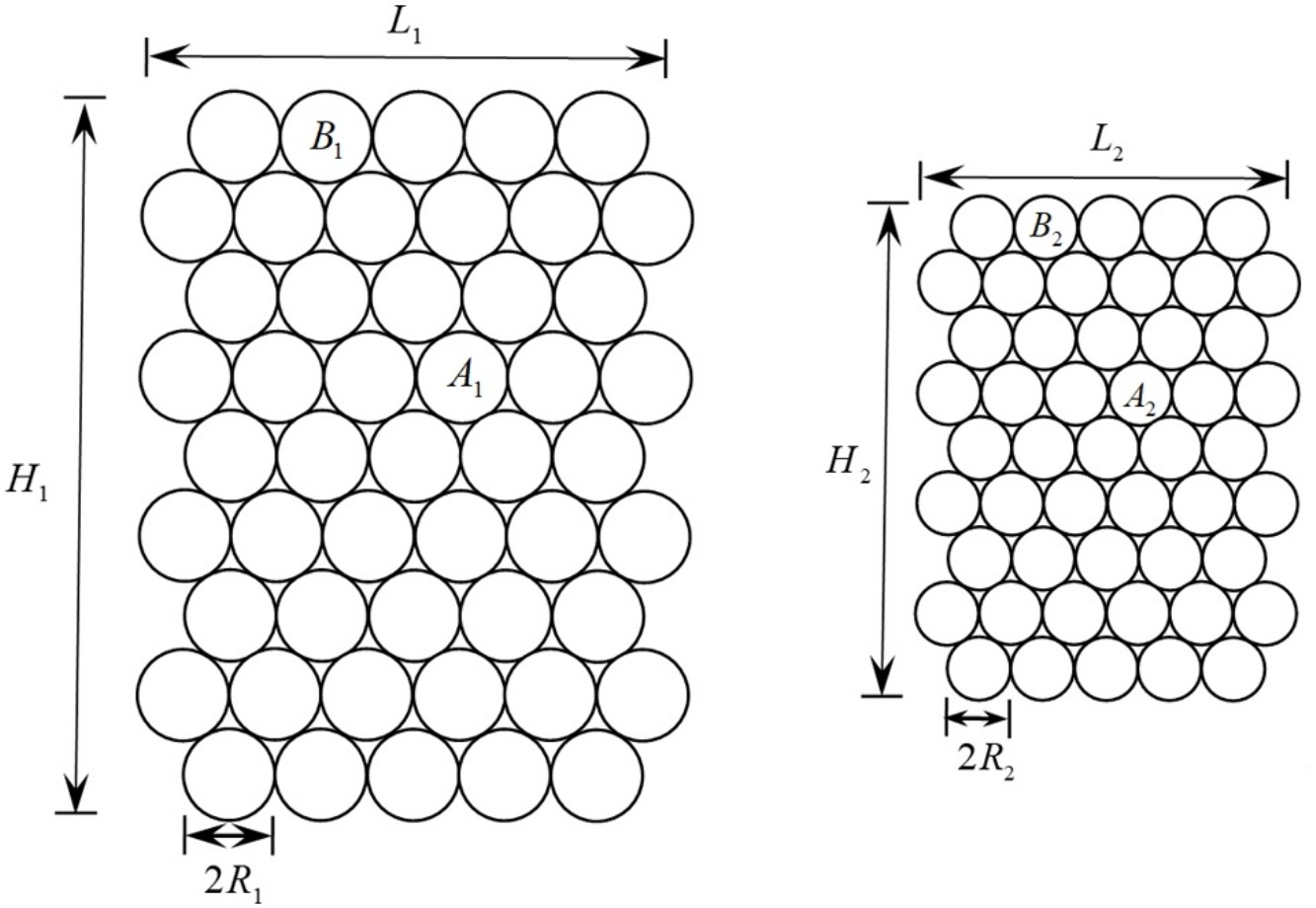
In this paper, dynamic similarity conditions are derived for discrete element simulations by non-dimensionalising the governing equations. These conditions must be satisfied so that the numerical model is a good representation of the physical phenomenon. For a pure mechanical system, if three independent ratios of the corresponding quantities between the two models are set, then the ratios of other quantities must be chosen according to the similarity principles. The scalability of linear and non-linear contact laws is also investigated. Numerical tests of 3D uni-axial compression are carried out to verify the theoretical results. Another example is presented to show how to calibrate the model according to laboratory data and similarity conditions. However, it is impossible to reduce computer time by scaling up or down certain parameters and continue to uphold the similarity conditions. The results in this paper provide guidelines to assist discrete element modelers in setting up the model parameters in a physically meaningful way.

Graphical abstract

Keywords

Discrete element method; Dimensionless analysis; Dynamic similarity; Parameter calibration; ESyS_Particle

文章导读