The divergence of nearby trajectories in soft-sphere DEM--颗粒学报PARTICUOLOGY

Fullmer, W. D., Porcu, R., Musser, J., Almgren, A. S., & Srivastava, I. (2022). The divergence of nearby trajectories in soft-sphere DEM. Particuology, 63, 1-8. https://doi.org/10.1016/j.partic.2021.06.008

The divergence of nearby trajectories in soft-sphere DEM

William D. Fullmer^{a b *}, Roberto Porcu^{a b}, Jordan Musser^a, Ann S. Almgren^c, Ishan Srivastava^c

a National Energy Technology Laboratory, Morgantown, WV 26507, USA
b NETL Support Contractor, Morgantown, WV 26507, USA
c Center for Computational Sciences and Engineering, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA

10.1016/j.partic.2021.06.008

Volume 63, April 2022, Pages 1-8

Received 29 April 2021, Revised 11 June 2021, Accepted 19 June 2021, Available online 7 July 2021, Version of Record 10 September 2021.

E-mail: william.fullmer@netl.doe.gov

Highlights

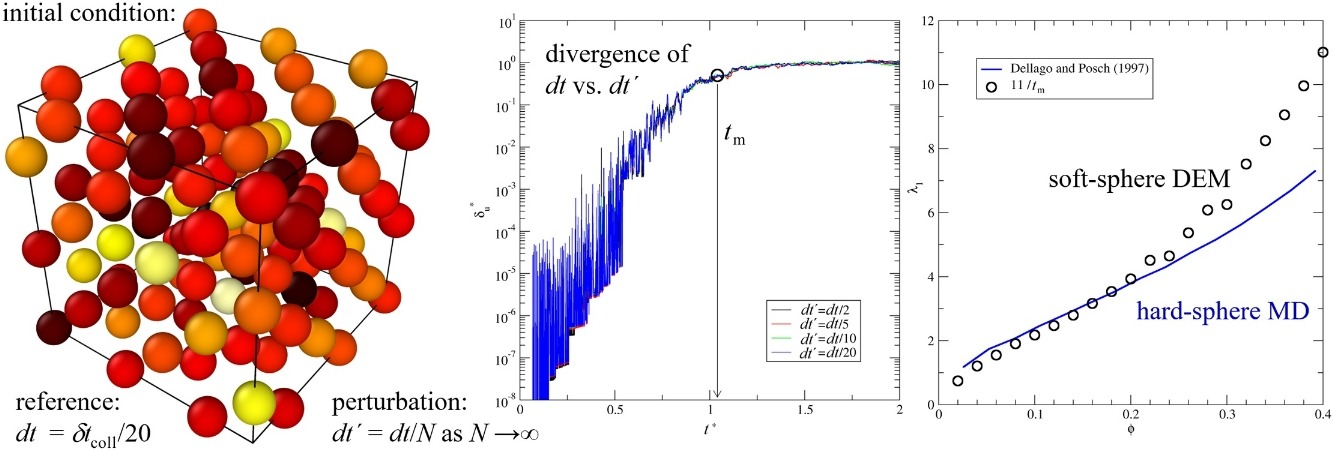
• Chaos in granular gas is studied by soft-sphere Discrete Element Method (DEM).

• Degree of instability is quantified by calculating the dynamical memory time.

• Soft-sphere DEM shows higher degree of instability than hard-sphere MD.

• Application as a DEM code development test is demonstrated.

Abstract

The n-body instability is investigated with the soft-sphere discrete element method. The divergence of nearby trajectories is quantified by the dynamical memory time. Using the inverse proportionality between the dynamical memory time and the largest Lyapunov exponent, the soft-sphere discrete element method results are compared to previous hard-sphere molecular dynamics data for the first time. Good agreement is observed at low concentrations and the degree of instability is shown to increase asymptotically with increasing spring stiffness. At particle concentrations above 30%, the soft-sphere Lyapunov exponents increase faster than the corresponding hard-sphere data. This paper concludes with a demonstration of how this case study may be used in conjunction with regression testing and code verification activities.

Graphical abstract

Keywords

Soft-sphere; DEM; Chaos; Lyapunov exponent

文章导读