Determining a representative element volume for DEM simulations of samples with non-circular particles--颗粒学报PARTICUOLOGY

Adesina, P., O’Sullivan, C., Morimoto, T., & Otsubo, M. (2022). Determining a representative element volume for DEM simulations of samples with non-circular particles. Particuology, 68, 29-43. https://doi.org/10.1016/j.partic.2021.10.007

Determining a representative element volume for DEM simulations of samples with non-circular particles

Peter Adesina^a *, Catherine O’Sullivan ^a, Tokio Morimoto ^a, Masahide Otsubo ^b

a Dept. of Civil and Environmental Engineering, Imperial College London, South Kensington, London SW7 2AZ, UK
b Institute of Industrial Science, The University of Tokyo, 4-6-1 Komaba Meguro-ku, Tokyo 153-8505, Japan

10.1016/j.partic.2021.10.007

Volume 68, September 2022, Pages 29-43

Received 2 July 2021, Revised 19 October 2021, Accepted 22 October 2021, Available online 12 November 2021, Version of Record 30 November 2021.

E-mail: p.adesina18@imperial.ac.uk; greatpetson121@gmail.com

Highlights

• Effects of particle shape and sample density on representative element volume (REV) for granular materials were investigated.

• The minimum REV reduces with increasing packing density.

• The minimum REV is sensitive to the characteristics measured.

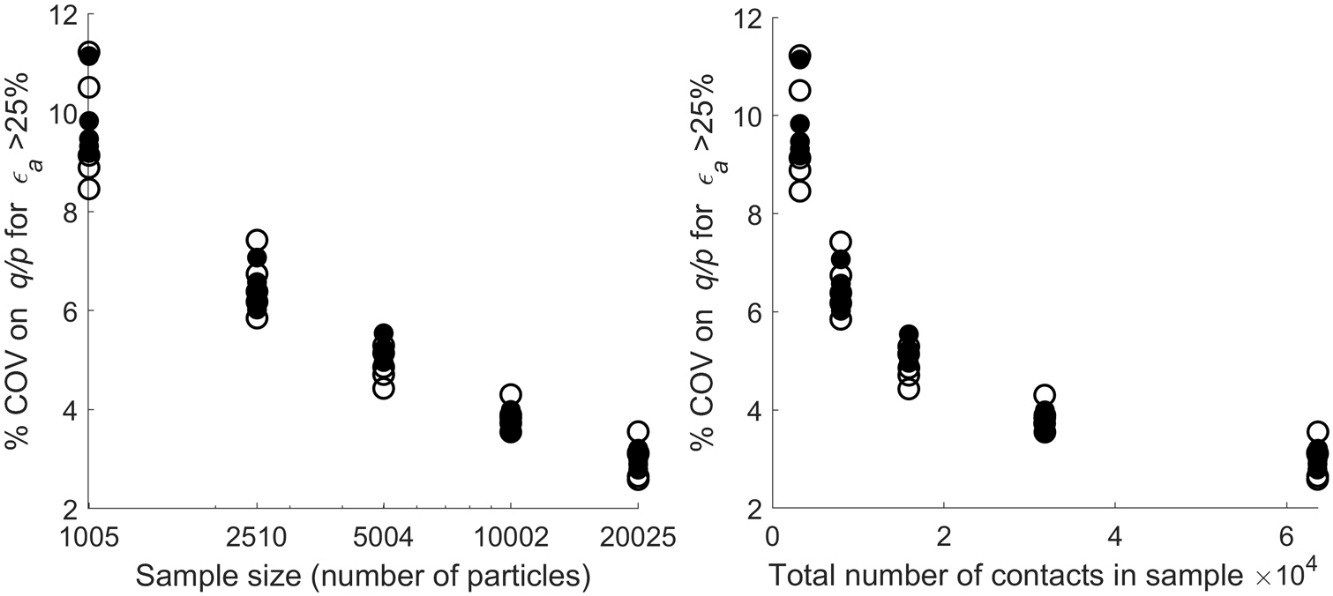
• Analysis of the fluctuations around the critical state stress ratio can be used to determine REV.

• Analysis of the number of contacts in samples indicates the effect of particle aspect ratio on REV.

Abstract

Numerical studies on the number of particles or system size required to attain a representative element volume (REV) for discrete element method (DEM) simulations of granular materials have almost always considered samples with spherical or circular particles. This study considers how many particles are needed to attain a REV for 2D samples of 2-disc cluster particles where the particle aspect ratio (AR) was systematically varied. Dense and loose assemblies of particles were simulated. The minimum REV was assessed both by considering the repeatability of static packing characteristics and the shearing behaviour in biaxial compression tests, and by investigating the effect of sample size on the measured characteristics and observed shearing behaviour. The repeatability of the data considered generally improved with increasing sample size. The packing characteristics of the dense samples were more repeatable suggesting that the minimum REV reduces with increasing packing density. The minimum REV was observed to be sensitive to the characteristic measured. Although the overall responses of the samples during shear deformation were similar irrespective of the sample sizes, the smaller the sample size, the higher the fluctuations observed in the responses. Analysis of the coefficient of variation of the fluctuations around the critical state stress ratio can provide insight as to whether a REV is attained. The particle AR influences the effect of sample size on shearing characteristics and thus the minimum number of particles required to attain a REV; this can be explained by the influence of AR on the number of contacts within the samples.

Graphical abstract

Keywords

DEM; Representative element volume; Non-circular particles; Particle shape; Granular materials

文章导读