Solution of Smoluchowski coagulation equation for Brownian motion with TEMOM--颗粒学报PARTICUOLOGY

Xie, M., & He, Q. (2022). Solution of Smoluchowski coagulation equation for Brownian motion with TEMOM. Particuology, 70, 64-71. https://doi.org/10.1016/j.partic.2022.01.006

Solution of Smoluchowski coagulation equation for Brownian motion with TEMOM

Mingliang Xie ^a^*, Qing He ^b *

a State Key Laboratory of Coal Combustion, Huazhong University of Science and Technology, Wuhan 430074, China
b Guangdong Provincial Key Laboratory of Distributed Energy Systems, School of Chemical Engineering and Energy Technology, Dongguan University of Technology, Dongguan 523808, China

10.1016/j.partic.2022.01.006

Volume 70, November 2022, Pages 64-71

Received 3 November 2021, Revised 1 January 2022, Accepted 5 January 2022, Available online 19 January 2022, Version of Record 31 January 2022.

E-mail: mlxie@mail.hust.edu.cn; heqing@dgut.edu.cn

Highlights

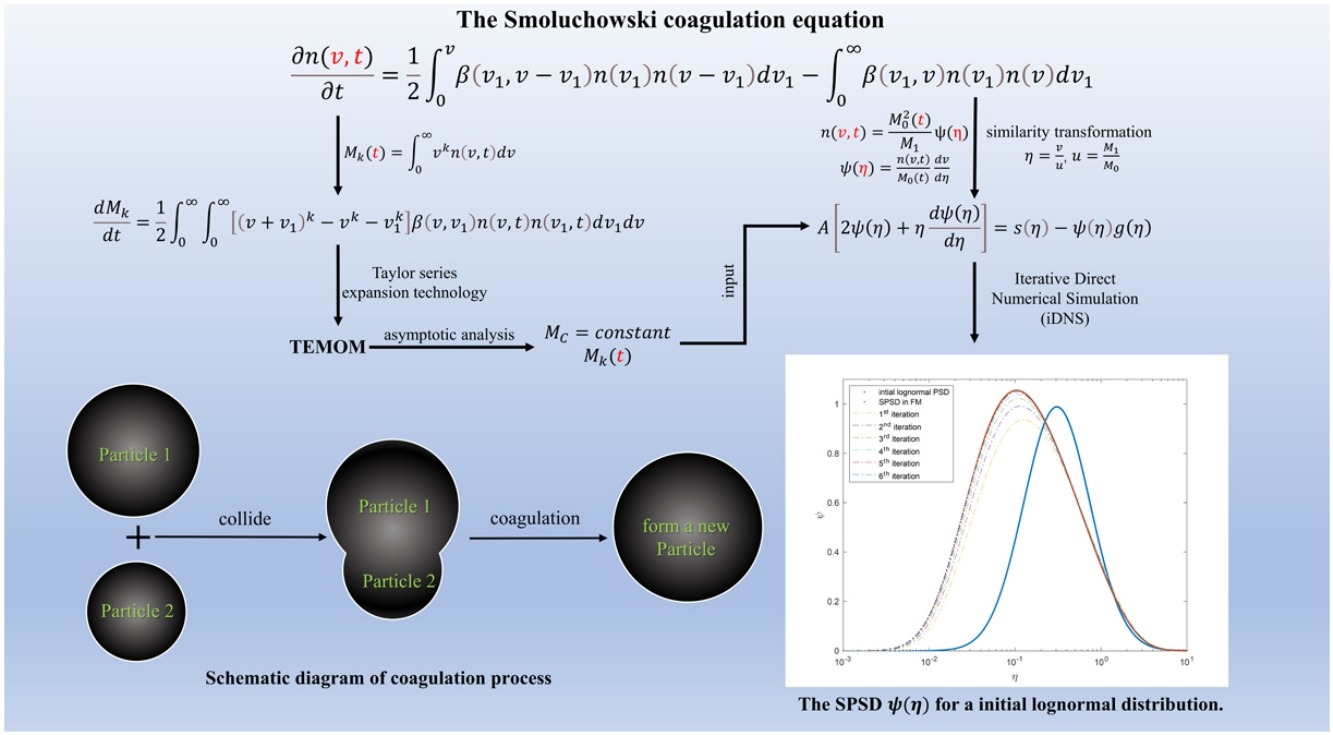
• A simple iterative direct numerical simulation (iDNS) for similarity solution is proposed.

• Convergence and accuracy of the numerical method are verified.

• A bridge between Taylor-series expansion method of moment (TEMOM) and similarity theory is constructed by iDNS.

• TEMOM provides a complete solution for solving Smoluchowski coagulation equation.

Abstract

The particle number density in the Smoluchowski coagulation equation usually cannot be solved as a whole, and it can be decomposed into the following two functions by similarity transformation: one is a function of time (the particle k-th moments), and the other is a function of dimensionless volume (self-preserving size distribution). In this paper, a simple iterative direct numerical simulation (iDNS) is proposed to obtain the similarity solution of the Smoluchowski coagulation equation for Brownian motion from the asymptotic solution of the k-th order moment, which has been solved with the Taylor-series expansion method of moment (TEMOM) in our previous work. The convergence and accuracy of the numerical method are first verified by comparison with previous results about Brownian coagulation in the literature, and then the method is extended to the field of Brownian agglomeration over the entire size range. The results show that the difference between the lognormal function and the self-preserving size distribution is significant. Moreover, the thermodynamic constraint of the algebraic mean volume is also investigated. In short, the asymptotic solution of the TEMOM and the self-preserving size distribution form a one-to-one mapping relationship; thus, a complete method to solve the Smoluchowski coagulation equation asymptotically is established.

Graphical abstract

Keywords

Population balance equation; Particle size distribution; Moment method; Similarity solution; Brownian motion

文章导读