DEM analysis of passive arching in a shallow trapdoor under eccentric loading--颗粒学报PARTICUOLOGY

Zhang, R., Su, D., Lin, X., Lei, G., & Chen, X. (2023). DEM analysis of passive arching in a shallow trapdoor under eccentric loading. Particuology, 77, 14-28. https://doi.org/10.1016/j.partic.2022.08.004

DEM analysis of passive arching in a shallow trapdoor under eccentric loading

Ruixiao Zhang ^{a b}, Dong Su ^{a b c *}, Xingtao Lin ^{a b}, Guoping Lei ^d, Xiangsheng Chen ^{a b c}

a Key Laboratory for Resilient Infrastructures of Coastal Cities (MOE), Shenzhen University, Shenzhen, 518060, China
b College of Civil and Transportation Engineering, Shenzhen University, Shenzhen, 518060, China
c Shenzhen Key Laboratory of Green, Efficient and Intelligent Construction of Underground Metro Station, Shenzhen University, Shenzhen, 518060, China
d School of Transportation, Civil Engineering & Architecture, Foshan University, Foshan, 528225, China

10.1016/j.partic.2022.08.004

Volume 77, June 2023, Pages 14-28

Received 3 January 2022, Revised 23 July 2022, Accepted 1 August 2022, Available online 18 August 2022, Version of Record 2 December 2022.

E-mail: sudong@szu.edu.cn

Highlights

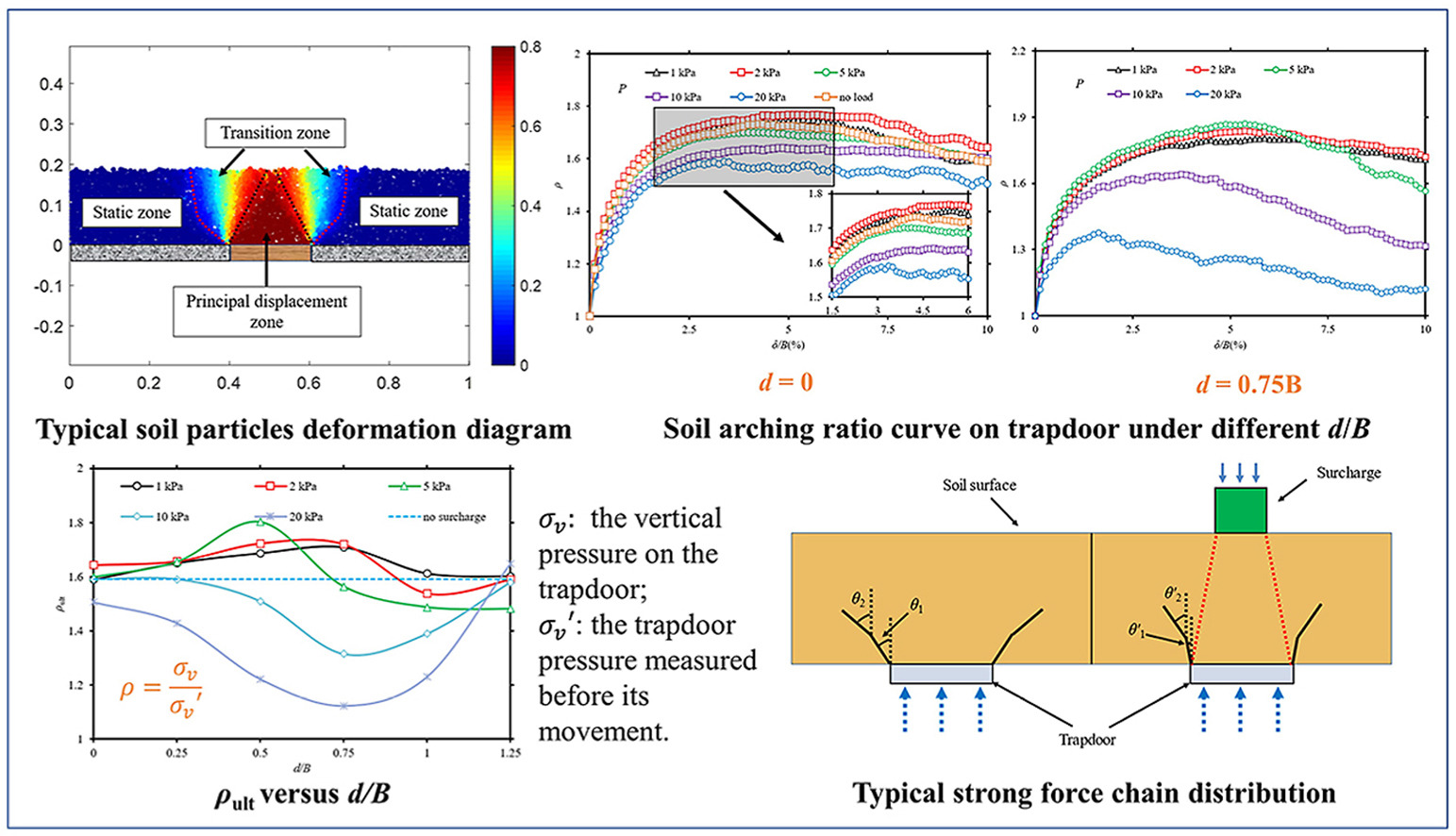
• Evolution mechanism of passive arching under eccentric loading is investigated.

• The passive arching effect is degraded by a surcharge.

• Ultimate soil arching ratio could be approximated as a W-shaped distribution along + x-direction.

• The force chain on the trapdoor expands outward to form an inverted funnel shape.

• The most powerful force on the trapdoor is mainly distributed on its edge.

Abstract

This study analyzed the passive arching effect under eccentric loading by developing a series of trapdoor discrete numerical models. The numerical models were validated by comparison with laboratory test results. The deformation pattern, soil arching ratio, force chain distribution, and coordination number under various surcharge magnitudes and deviation distances were analyzed. The numerical results showed that the deformation diagram of soil particles can be divided into three zones: principal displacement zone, transition zone, and static zone. With an increase in the surcharge magnitude, the range of the principal displacement zone decreased, but the range of the transition region increased. The curve of the soil arching ratio on the trapdoor can be divided into three phases, which can be well characterized by the tangent modulus. The passive arching effect is degraded by a surcharge. The ultimate soil arching ratio could be approximated as a W-shaped distribution along the +x-direction. With an increase in the trapdoor displacement, the force chain on the trapdoor gradually expanded outward to form an inverted funnel shape. The most powerful force on the trapdoor was mainly distributed on its edge. The average coordination number decreased gradually as the trapdoor moved upward.

Graphical abstract

Keywords

Passive arching; Eccentric load; Discrete element method; Force chain distribution; Trapdoor apparatus

文章导读