Incorporating truncated fractal distribution into Maxwell model to quantify thermal conductivity and its uncertainty in heterogeneous multiparticle systems--颗粒学报PARTICUOLOGY

Zhu, J. (2023). Incorporating truncated fractal distribution into Maxwell model to quantify thermal conductivity and its uncertainty in heterogeneous multiparticle systems. Particuology, 80, 81-89. https://doi.org/10.1016/j.partic.2022.11.016

Incorporating truncated fractal distribution into Maxwell model to quantify thermal conductivity and its uncertainty in heterogeneous multiparticle systems

Jianting Zhu ^*

Department of Civil and Architectural Engineering and Construction Management, University of Wyoming, Laramie, WY, 82071, USA

10.1016/j.partic.2022.11.016

Volume 80, September 2023, Pages 81-89

Received 24 October 2022, Revised 22 November 2022, Accepted 23 November 2022, Available online 7 December 2022, Version of Record 1 March 2023.

E-mail: jzhu5@uwyo.edu

Highlights

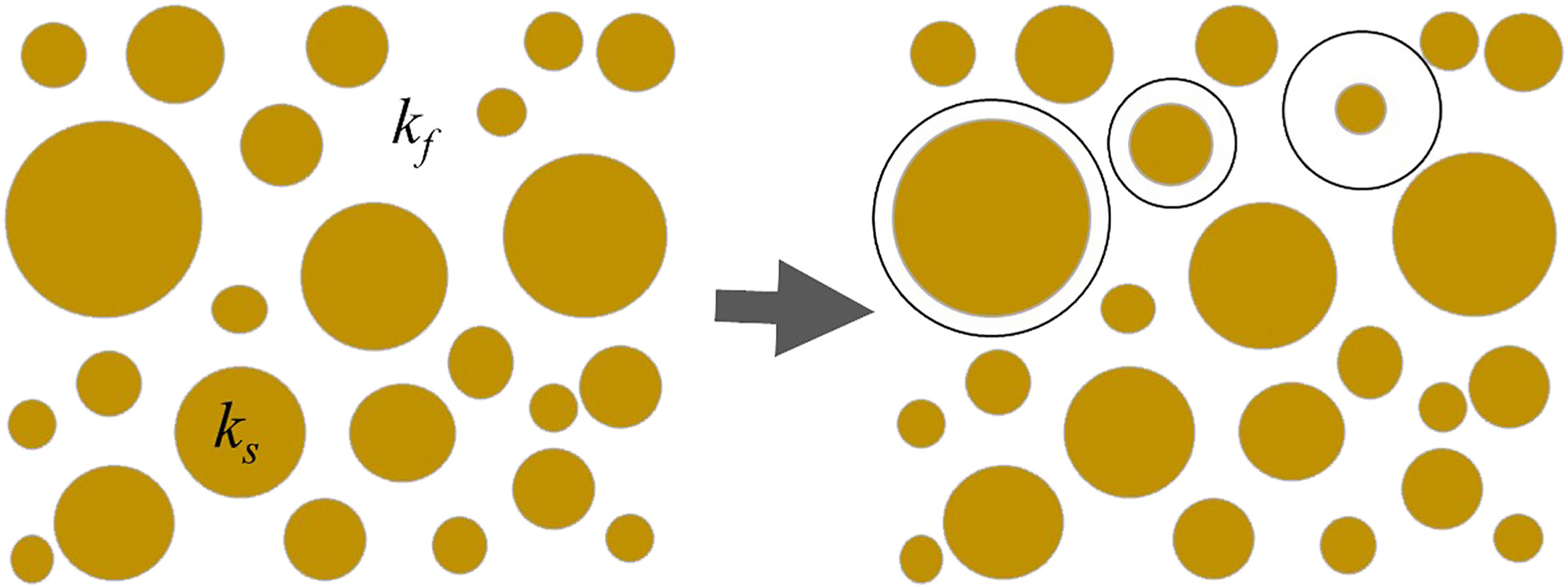
• Truncated fractal distribution is integrated into the Maxwell thermal conductivity model.

• Fractal parameters are constrained based on the void fraction of heterogeneous multiparticle system.

• Incorporating fraction fractal distribution can better capture scatters in experimental results.

• Thermal conductivity and its standard deviation decrease with increasing fractal dimensions.

Abstract

An approach is developed to examine the mean and uncertainty of thermal conductivity of a heterogeneous multiparticle system, where the particle concentration or void fraction is treated as a truncated fractal distribution. The truncated fractal distribution is then integrated into the Maxwell model, which is equivalent to a cell model in which the multiparticle system is conceptualized as a spherical fluid cell that envelopes a solid particle. The developed mean thermal conductivity is compared with four experimental data sets of liquid-saturated media from the literature. The effect of fractal characteristics is quantified and discussed. Incorporating particle concentration or void fraction truncated fractal distribution can better capture scatters in the experimental results. The thermal conductivity and its standard deviation decrease with increasing fractal dimensions. When the void fraction is truncated fractal, the uncertainty increases mostly in the low mean void fraction range and drops more quickly with the increasing mean void fraction compared to the case where the particle concentration is truncated fractal. In a typical case of multiparticle system when the solid particles are more conductive than the fluid, the faster increase rate of standard deviation with the ratio of solid over fluid conductivities occurs when the mean void fraction is smaller.

Graphical abstract

Keywords

Thermal conductivity; Heterogeneous multiparticle system; Truncated fractal distribution; Particle concentration; Void fraction

文章导读