DEM simulations of critical state behaviour of granular materials under various drained triaxial stress path tests--颗粒学报PARTICUOLOGY

Kodicherla, S. P. K., Gong, G., & Wilkinson, S. (2023). DEM simulations of critical state behaviour of granular materials under various drained triaxial stress path tests. Particuology, 81, 98-108. https://doi.org/10.1016/j.partic.2022.12.015

DEM simulations of critical state behaviour of granular materials under various drained triaxial stress path tests

Shiva Prashanth Kumar Kodicherla ^a *, Guobin Gong ^b *, Stephen Wilkinson ^c *

a Department of Civil, Mining and Process Engineering, Namibia University of Science and Technology, Windhoek, Namibia
b Department of Civil Engineering, Xi’an Jiaotong-Liverpool University, Suzhou, China
c Faculty of Engineering and Information Sciences, University of Wollongong, Dubai Campus, Dubai, United Arab Emirates

10.1016/j.partic.2022.12.015

Volume 81, October 2023, Pages 98-108

Received 31 August 2022, Revised 3 December 2022, Accepted 21 December 2022, Available online 16 January 2023, Version of Record 19 January 2023.

E-mail: prashanthetc1024@gmail.com, Guobin.Gong@xjtlu.edu.cn, 2stephen.wilkinson@gmail.com

Highlights

• Unique deviator stress at critical state for a given initial confining pressure under axial compression.

• Unique critical coordination number (CN) independent of stress paths for a given initial confining pressure.

• Increase of critical CN correlated to decrease in critical void ratio as initial confining pressures increase.

• Unique linear relationship between critical coordination numbers and critical state void ratios.

• Unique polynomial relationship between critical coordination numbers and mean effective stresses.

Abstract

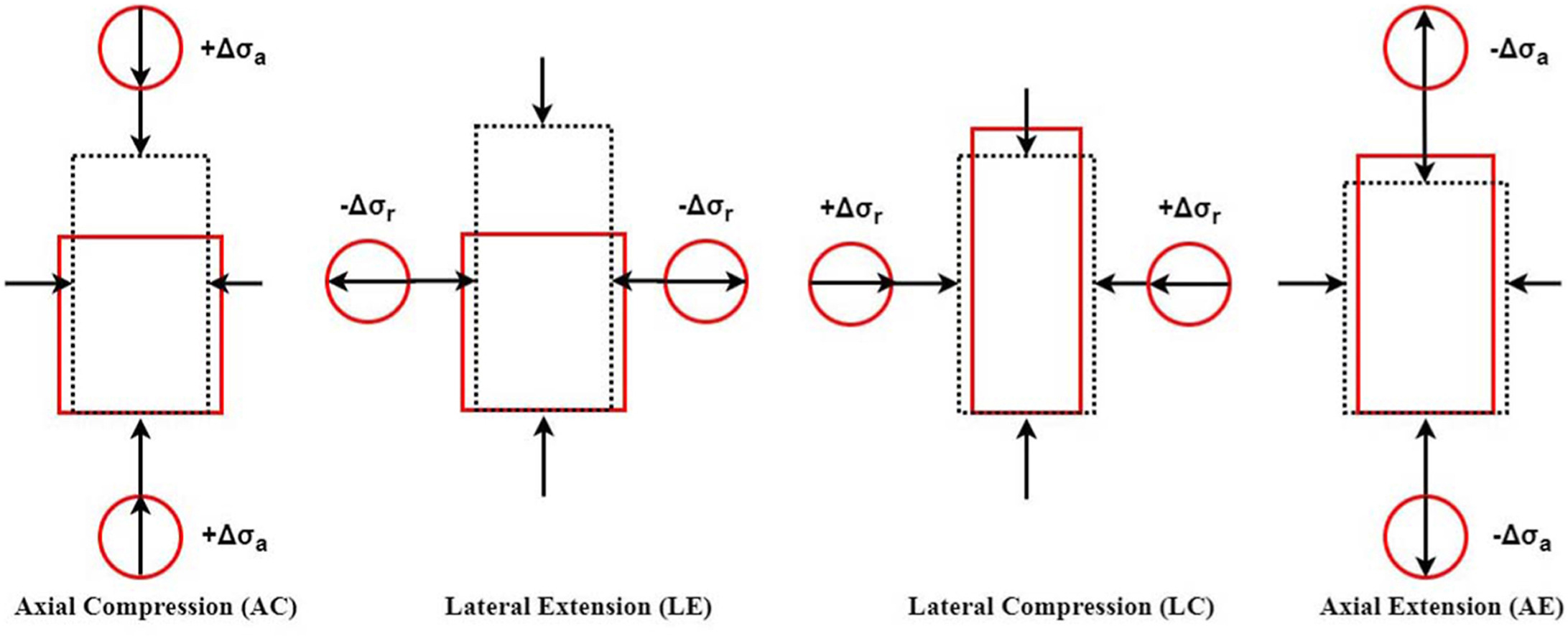
The present study investigates the critical state behaviour of granular assemblies composed of clumped particles under four different drained axisymmetric triaxial stress paths, using the discrete element method (DEM). A series of numerical samples were prepared at initial states with different density indexes (I_D) and different initial confining pressures (p₀'). These samples were sheared to large strains, at which constant stresses and volumes were maintained to reach the critical state. The evolution of stress ratio under the same loading mode (for the same intermediate principal stress ratio, b) is shown to yield an almost identical behaviour independent of stress paths, whereas the stress-strain response depends on the stress paths. Four different axisymmetric stress paths all share the same unique friction angle at critical state, indicating the Mohr-Coulomb failure criterion is the appropriate critical state strength criterion, which is at least true for the axisymmetric stress conditions. A unique coordination number (CN) is achieved at the critical state for a given , which is independent of the stress path. The critical state CN is found to increase with the increase in , which could be attributed to the decrease in the critical state void ratio (e_c) as mean effective stress (p') increases. Interestingly, a unique linear functional relationship is found between the critical state values of CN and ec, and a unique polynomial functional relationship is found between the critical state values of CN and p'. These functional relationships indicate no dependency on the stress paths or loading modes, thus characterizing unique features at critical states at both macroscopic and microscopic levels for a given type of granular material.

Graphical abstract

Keywords

Discrete element method; Critical state; Drained behaviour; Triaxial stress paths

文章导读