DEM investigation of strength and critical state behaviours of granular materials under true triaxial loadings--颗粒学报PARTICUOLOGY

Zhu, M., Gong, G., Xia, J., & Wilkinson, S. (2024). DEM investigation of strength and critical state behaviours of granular materials under true triaxial loadings. Particuology, 85, 198-212. https://doi.org/10.1016/j.partic.2023.04.004

DEM investigation of strength and critical state behaviours of granular materials under true triaxial loadings

Minyi Zhu ^{a b}, Guobin Gong ^a *, Jun Xia ^a, Stephen Wilkinson ^c

a Department of Civil Engineering, Xi'an Jiaotong – Liverpool University, China
b Department of Civil Engineering and Industrial Design, University of Liverpool, Liverpool, UK
c Faculty of Engineering and Information Sciences, University of Wollongong in Dubai, United Arab Emirates

10.1016/j.partic.2023.04.004

Volume 85, February 2024, Pages 198-212

Received 26 January 2023, Revised 31 March 2023, Accepted 11 April 2023, Available online 29 April 2023, Version of Record 8 May 2023.

E-mail: Guobin.Gong@xjtlu.edu.cn

Highlights

• Uniqueness of critical state line and strength behaviour under true triaxial conditions are studied.

• Different loading modes and confining pressures are considered.

• Both Satake and Matsuoka criteria can appropriately represent critical state strength.

Abstract

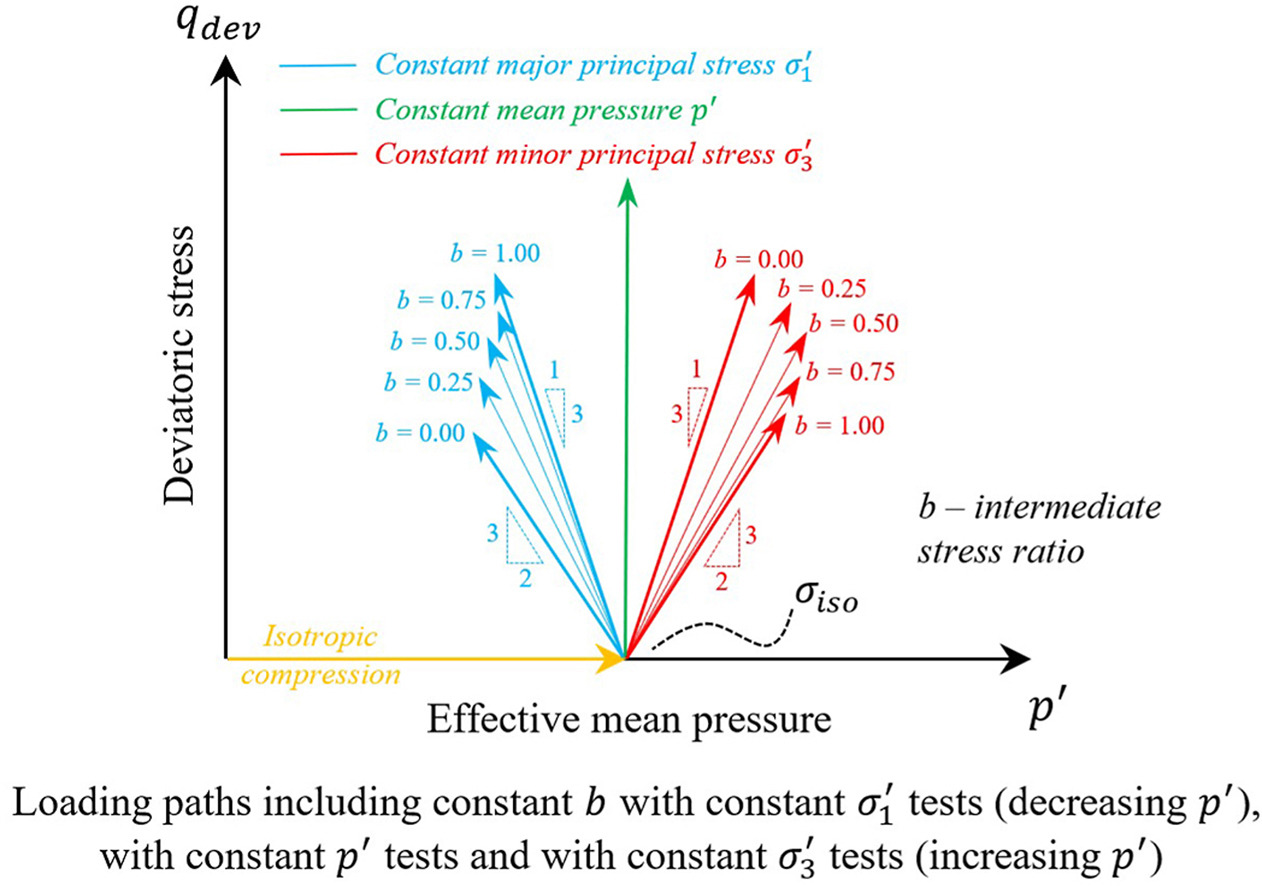
This paper investigates the strength and critical state (CS) behaviours of granular materials via DEM simulations of true triaxial drained tests under three different loading modes including constant b (intermediate stress ratio) tests with constant σ₁^' (major principal stress), constant p^' (mean pressure) and constant σ₃^' (minor principal stress) respectively. To this end, a series of samples are generated with the same particle size distribution, and with the confining stresses ranging from 100 kPa to 900 kPa. The CS is achieved for all samples. Both the macroscopic behaviours and the microscopic behaviours are examined and compared considering different loading modes, confining stresses and intermediate stress ratios (b). The critical state lines (CSLs) are found to be unique and independent of the loading modes, but dependent on the b values. The CSLs with b = 0 and b=1 form the two boundaries of CSLs respectively beyond which CSLs under all other b tests cannot go beyond. Six different strength criteria are examined and compared in terms of both peak and CS failures. The Mohr–Coulomb strength criterion is found to be only suitable for axisymmetric loading conditions. The Lade-Duncan criterion is only suitable for describing peak strengths, which is dependent on the loading modes and confining stresses. The Satake criterion and Matsuoka-Nakai criterion are the more appropriate strength criteria for describing CS failures, indicating that the CS values of both the Satake parameter and the Matsuoka-Nakai parameter describe an inherent property that characterizes the CS failure for a given type of soil. The CS mechanical coordination number is fitted by a curved line for a given b value, which is unique regardless of the loading modes. The peak and CS values of both major and minor principal fabric tensors decrease with increasing b values, while they increase with increasing b values for the intermediate principal fabric tensor.

Graphical abstract

Keywords

Discrete element method; Intermediate stress ratio; Dilation; Critical state; Failure criterion

文章导读