A method to determine the bonded-particle model parameters for simulation of ores--颗粒学报PARTICUOLOGY

Wu, S., Wang, G., Fan, L., Guan, W., Guo, J., Liu, Z., & Wang, Y. (2024). A method to determine the bonded-particle model parameters for simulation of ores. Particuology, 86, 24-38. https://doi.org/10.1016/j.partic.2023.04.007

A method to determine the bonded-particle model parameters for simulation of ores

Shuwei Wu, Guoqiang Wang, Longfei Fan, Wei Guan, Jianbo Guo, Zhengbin Liu, Yukuan Wang ^*

School of Mechanical and Aerospace Engineering, Jilin University, Changchun, 130025, China

10.1016/j.partic.2023.04.007

Volume 86, March 2024, Pages 24-38

Received 10 February 2023, Revised 24 March 2023, Accepted 24 April 2023, Available online 5 May 2023, Version of Record 11 May 2023.

E-mail: ykwang21@mails.jlu.edu.cn

Highlights

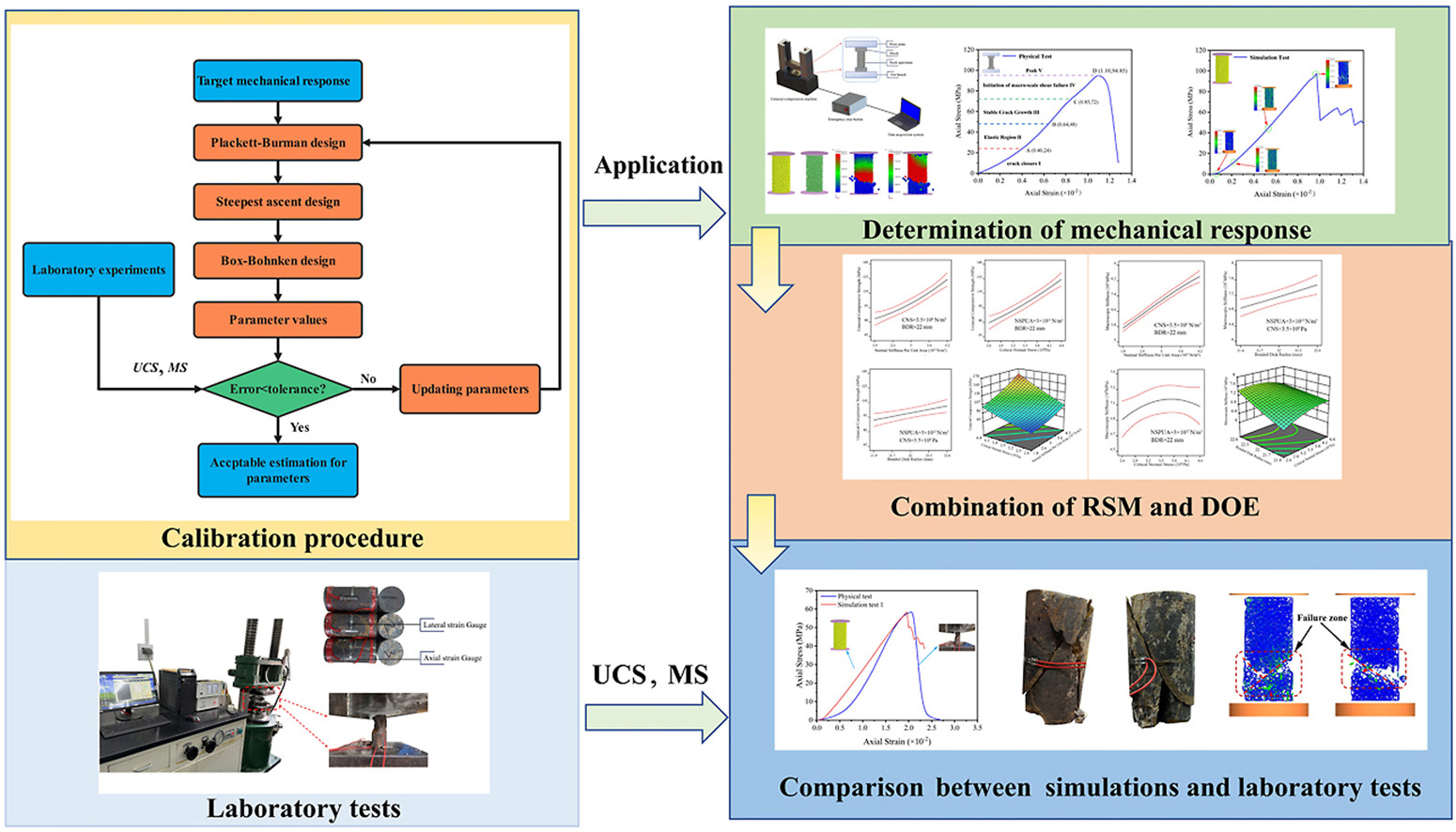
• A method of bonded-particle model calibration for ores is proposed.

• Connections between micro parameters and mechanical responses are determined.

• Sensitivities of micro parameters are explored by Plackett‒Burman design.

• Mathematical model is established.

Abstract

The bonded-particle model (BPM) is commonly used in the numerical analysis of ore samples. To improve the accuracy of simulating the mechanical process of ore process of ore crushing in a crusher, the parameters of the BPM for the ore must be calibrated. In this study, a calibration method was proposed for the scientific determination of the parameters of the BPM for ore undergoing uniaxial compression. First, physical tests and simulations were conducted to determine the mechanical response (uniaxial compressive strength and macroscopic stiffness) of ore during uniaxial compression. Then, the sensitivity of the mechanical response to the values of microscopic parameters was tested using a Plackett‒Burman design. Next, the microscopic parameters with the greatest impact on the response were identified, and the range of parameters that met the target response was determined using a steepest ascent design; Second, a second-order model of the mechanical response was established using the sensitive parameters by combining a Box‒Behnken design with response surface methodology to obtain the optimal BPM parameters. Simulation tests showed that the normal stiffness per unit area, critical shear stress, and bonded disk radius had significant effects on the uniaxial compressive strength (UCS) and macroscopic stiffness (MS). To verify the validity of the proposed calibration method, laboratory tests were conducted. The consistency of the simulation results with experimental results indicated that response surface methodology with the Plackett‒Burman design, steepest ascent design, and Box‒Behnken design can be an effective method for calibrating the BPM of ores.

Graphical abstract

Keywords

Bonded-particle model; Discrete element method; Calibration method; Design of experiment; Uniaxial compression test

文章导读