Kinetic model of vibration screening for granular materials based on biological neural network--颗粒学报PARTICUOLOGY

Zhao, Z., Zhang, Y., Qin, F., & Jin, M. (2024). Kinetic model of vibration screening for granular materials based on biological neural network. Particuology, 88, 98-106. https://doi.org/10.1016/j.partic.2023.08.017

Kinetic model of vibration screening for granular materials based on biological neural network

Zhan Zhao^a *, Yan Zhang ^a, Fang Qin ^{a b}, Mingzhi Jin ^a

a School of Agricultural Engineering, Jiangsu University, Zhenjiang, 212013, China
b Shandong Academy of Agricultural Machinery Sciences, Ji'nan, 250100, China

10.1016/j.partic.2023.08.017

Volume 88, May 2024, Pages 98-106

Received 28 March 2023, Revised 24 June 2023, Accepted 24 August 2023, Available online 15 September 2023, Version of Record 6 November 2023.

E-mail: zhaozhan@ujs.edu.cn

Highlights

• Kinetic model of vibration screening using bio-inspired neural network is proposed.

• Differential equation describing the neural dynamic characteristics is derived.

• Relationship between actual screening parameters and model coefficients is established.

• Feasibility and advantage of the proposed method are demonstrated.

Abstract

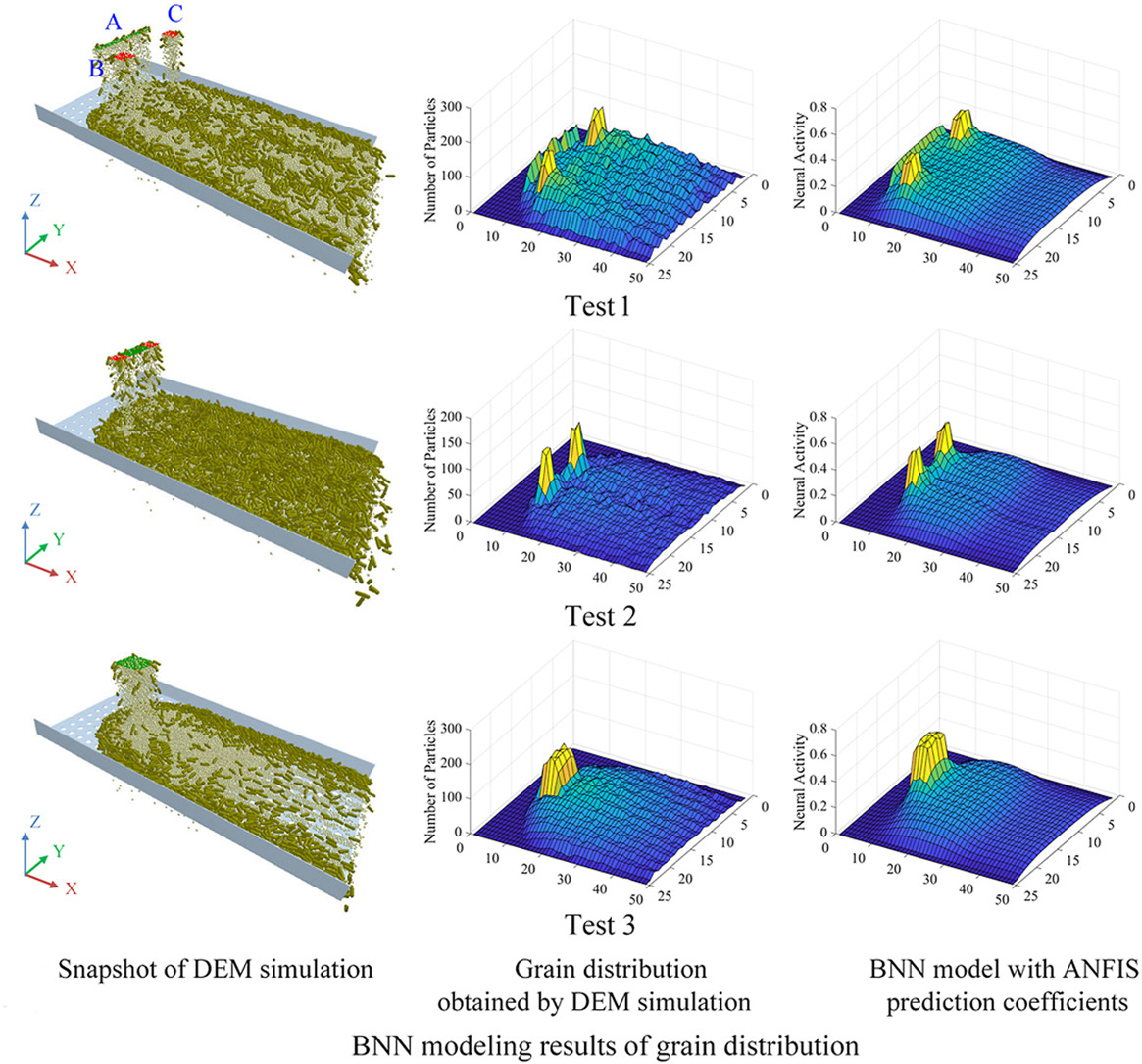
The kinetic model is the theoretical basis for optimizing the structure and operation performance of vibration screening devices. In this paper, a biological neurodynamic equation and neural connections were established according to the motion and interaction properties of the material under vibration excitation. The material feeding to the screen and the material passing through apertures were considered as excitatory and inhibitory inputs, respectively, and the generated stable neural activity landscape was used to describe the material distribution on the 2D screen surface. The dynamic process of material vibration screening was simulated using discrete element method (DEM). By comparing the similarity between the material distribution established using biological neural network (BNN) and that obtained using DEM simulation, the optimum coefficients of BNN model under a certain screening parameter were determined, that is, one relationship between the BNN model coefficients and the screening operation parameters was established. Different screening parameters were randomly selected, and the corresponding relationships were established as a database. Then, with straw/grain ratio, aperture diameter, inclination angle, vibration strength in normal and tangential directions as inputs, five independent adaptive neuro-fuzzy inference systems (ANFIS) were established to predict the optimum BNN model coefficients, respectively. The training results indicated that ANFIS models had good stability and accuracy. The flexibility and adaptability of the proposed BNN method was demonstrated by modeling material distribution under complex feeding conditions such as multiple regions and non-uniform rate.

Graphical abstract

Keywords

Kinetic model; Material distribution; Vibration screening; Biological neural network; DEM simulation; Adaptive neuro-fuzzy inference systems

文章导读