Implementation and validation of a bonded particle model to predict rheological properties of viscoelastic materials (Open Access)--颗粒学报PARTICUOLOGY

Mascara, M., Mayrhofer, A., Radl, S., & Kloss, C. (2024). Implementation and validation of a bonded particle model to predict rheological properties of viscoelastic materials. Particuology, 89, 198-210. https://doi.org/10.1016/j.partic.2023.11.001

Implementation and validation of a bonded particle model to predict rheological properties of viscoelastic materials (Open Access)

Michael Mascara ^{a b *}, Arno Mayrhofer ^b, Stefan Radl ^a *, Christoph Kloss ^b

a Institute of Process and Particle Engineering, Graz University of Technology, Inffeldgasse 13, Graz, 8010, Austria
b DCS Computing GmbH, Industriezeile 35, Linz, 4020, Austria

10.1016/j.partic.2023.11.001

Volume 89, June 2024, Pages 198-210

Received 6 April 2023, Revised 23 October 2023, Accepted 1 November 2023, Available online 15 November 2023, Version of Record 8 December 2023.

E-mail: michael.mascara@dcs-computing.com; radl@tugraz.at

Highlights

• New DEM based model implemented to account for materials behaving viscoelastically.

• Accuracy and validity of the model tested against analytical solutions of simple mechanical tests.

• Calibration of the model parameters on a wide range of materials with different behavior showing good flexibility.

• Good agreement between simulation and experimental data both in simple and complex systems for multiple materials.

Abstract

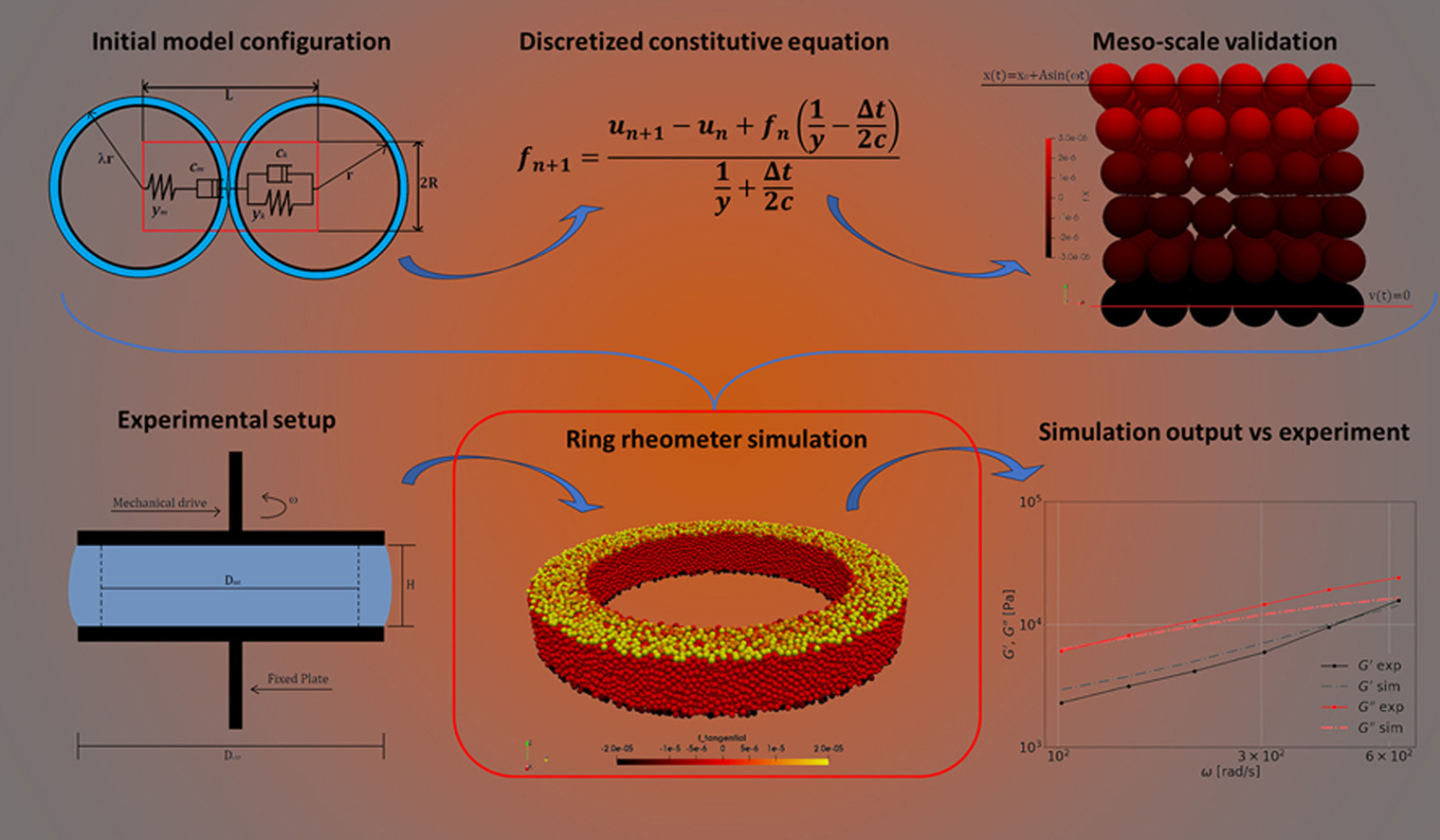
This work focuses on implementing a particle-based method able to characterize viscoelastic materials whose rheological properties, such as storage modulus G' and loss modulus G'', are known. It is based on the bonded particle model, with the elastic constitutive relation here substituted with a viscoelastic one to capture time-scale effects. The Burgers model, vastly used in literature to model viscoelastic systems, is discretized and implemented. The test case used for calibration comprises of a cubic lattice, sheared with a periodic motion, to mimic the effect of a shear rheometer. After appropriate filtering of the stress response, the rheological properties are obtained, highlighting the effect of the lattice geometry, as well as the particle size, on the accuracy of the model. Moreover, the Burgers parameters are calibrated by analytically fitting the experimental dataset, showing the limitation of the Burgers model. The micro-contact parameters are obtained from the macro parameters through appropriate scaling. After completing a frequency sweep, the simulated G' and G'' show a relatively large error, around 25% for G’ for example. For this reason, a more robust model, namely the generalized Maxwell model, has been implemented. The calibration procedure is performed in the same fashion as for the Burgers model. Moreover, the tangential micro-contact parameters are scaled w.r.t. the normal ones. This scaling parameter, called α, is calibrated by minimizing the root mean square error between simulation and experimental data, giving errors below 10% in both G′ and G″ for a large dataset. Additionally, a full ring plate-plate rheometer setup is simulated, and the simulation is compared with the given experimental dataset, again finding a good agreement.

Graphical abstract

Keywords

DEM; Rheology; Numerical modeling; Viscoelasticity

文章导读