
Predictions of the P1 approximation for radiative heat transfer in heterogeneous granular media (Open Access)
Jelena Mačak*, Christoph Goniva, Stefan Radl
Keywords: CFD-DEM; Thermal radiation; Coarse-graining; P1; Pebble bed nuclear reactor
DOI: 10.1016/j.partic.2023.01.003
P1模型是OpenFOAM等CFD软件中常用于热辐射计算的模型,但是P1模型难以准确预测非均匀体系的热辐射情况。为了提升P1模型在非均匀体系中的适用性,近期,奥地利DCS计算有限公司的Jelena Mačak、Christoph Goniva工程师和格拉茨理工大学的Stefan Radl副教授对此展开了深入研究。他们采用平滑辐射扩散率和添加伪散射项的方法对P1模型进行修正来减轻非均匀体系中固体体积分数发生突变处由于温度滑移而引发的热通量的非物理振荡,还结合CFD-DEM提出了一种包括对依赖性散射和粗粒化进行封闭的P1模型,并进一步验证了P1模型对单分散、双分散及多分散体系及粗粒化的适用性。
本文已OA,欢迎感兴趣的读者扫描下方二维码进入ScienceDirect官网阅读、下载!

研究背景
热辐射广泛存在于煤热解、生物质气化等化工反应过程中,并会产生显著的影响。为了更好的解析热辐射,精确的热辐射模型必不可少,而这通常会带来高昂的计算成本。目前,P1模型作为一种高效的热辐射模型被广泛应用于OpenFOAM等CFD软件中,但由于P1模型自身精度的缺陷,其难以预测流化床、回转窑等由于颗粒的空间波动而具有不均匀性的体系。因此,对P1模型进行修正并扩大其适用范围具有重要的意义。
研究方法
本文分别采用平滑辐射扩散率和添加伪散射项两种方法对P1模型进行修正,并结合CFD-DEM对依赖性散射和粗粒化进行封闭。P1模型是一种连续性模型,即将颗粒及其周围气体的混合物视为一种连续介质。因此,体系对热辐射的吸收率可视为颗粒和流体对热辐射吸收率的加和:
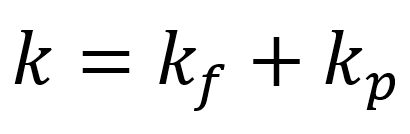
其中kf代表流体对热辐射的吸收率,kp代表颗粒对热辐射的吸收率。同理,体系对热辐射的散射率可以表示为:
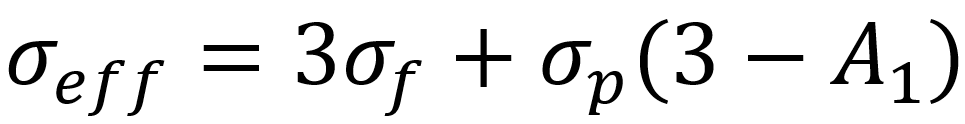
其中σf代表流体对热辐射的散射率,σp代表颗粒对热辐射的散射率,A1是平均散射角的余弦值。颗粒对于热辐射的耗散率βp、散射率σp及吸收率kp存在如下关系:
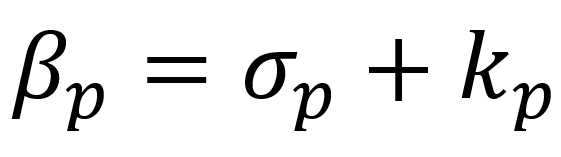
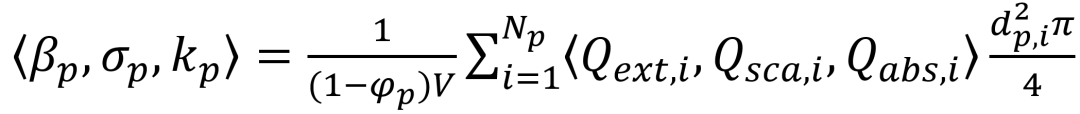
其中Qext,i、Qsca,i、Qabs,i分别是单个颗粒对热辐射的耗散、散射及吸收率,Np为颗粒数目,dp,i是第i个颗粒的直径,V为计算域的体积,考虑到周围粒子对辐射场的影响及所谓的依赖性散射,作者在上式中引入了1/(1–φp)项,其中φp为颗粒的体积分数。考虑到粗粒化的情况,作者还引入了颗粒包直径dCG和颗粒放大比例φCG = dCG/dp对上式进行修正:
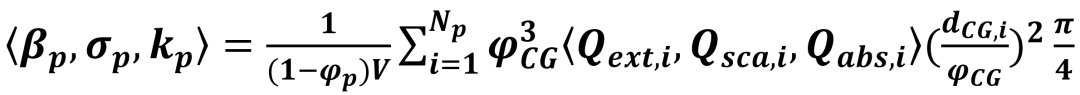
通过上述方程便可进一步求解P1模型:
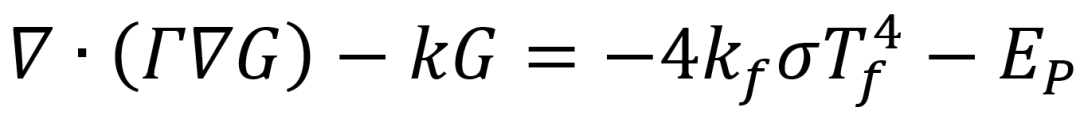
其中Γ是热辐射扩散率,kG是被颗粒和流体吸收的热辐射强度,4kfσTf4是流体释放出的热辐射强度,Ep是颗粒释放的热辐射强度。同时为了减轻热通量的非物理振荡,作者分别采用了求解∂Γ/∂t=D∇2Γ 来平滑辐射扩散率Γ,其中D=(Lsmooth2)/∆t是扩散系数,以及添加流体的伪散射项对体系的散射率进行修正的方法:
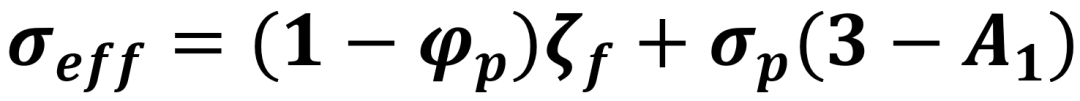
其中(1–φp)ζf为流体的伪散射项。
研究内容
本文借助OpenFOAM并采用P1模型分别计算了单分散、双分散及多分散体系在三种不同的光学厚度(τL)下热辐射强度沿x轴的分布情况并与解析解进行对比,结果表明P1模型对τL≫1下的单分散、双分散及多分散体系都具有很好的适用性。
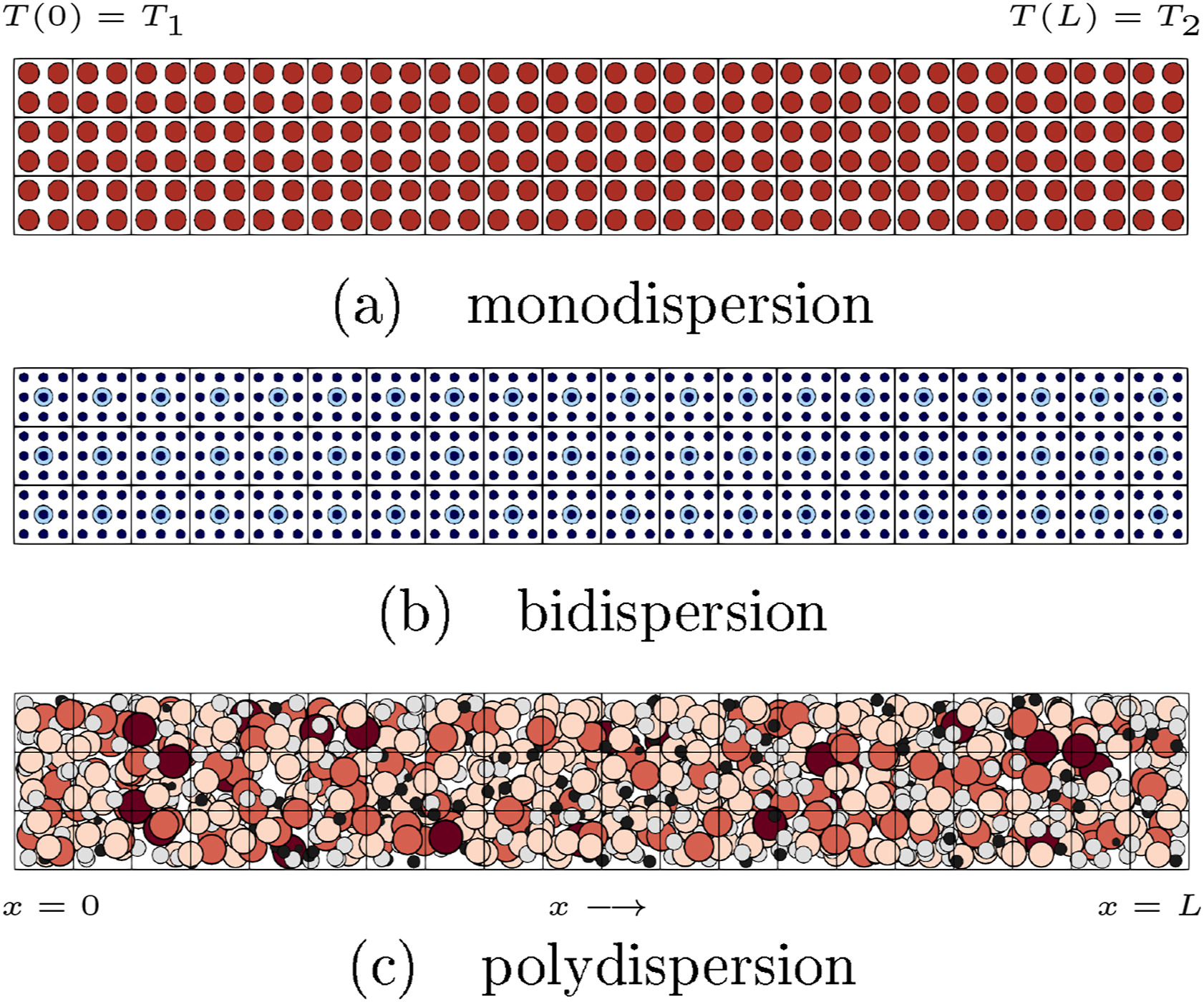
图1. 单分散、多分散及双分散体系的稳态模拟计算域
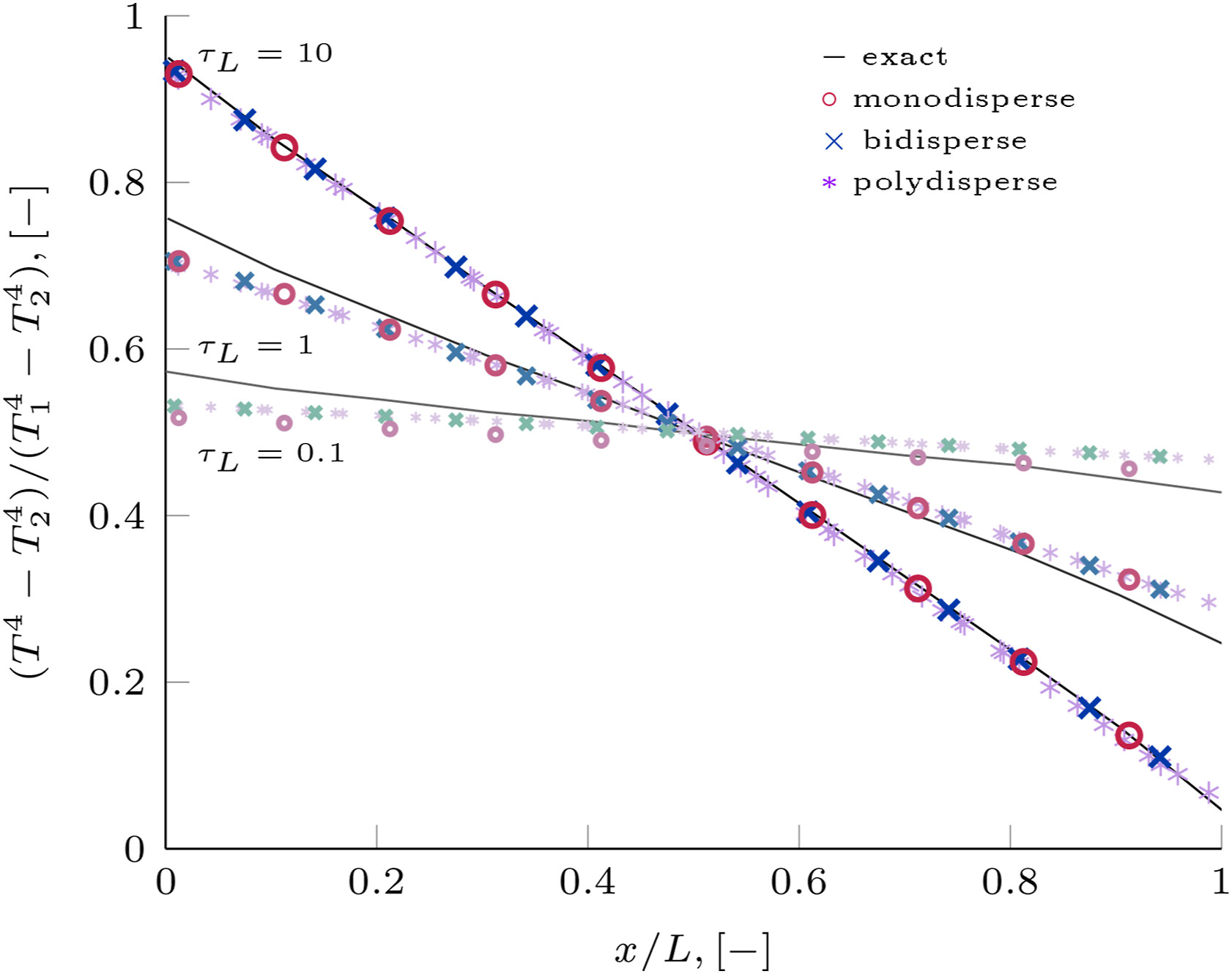
图2. 不同体系在不同光学厚度下沿x轴的辐射强度
本文也在φCG=1000及φCG=1000000两种粗粒化的情况下借助P1模型对τL=10时上述三种不同分散体系下沿x轴的热辐射强度进行计算并与解析解对比,结果表明P1模型对粗粒化也具有很好的适用性。
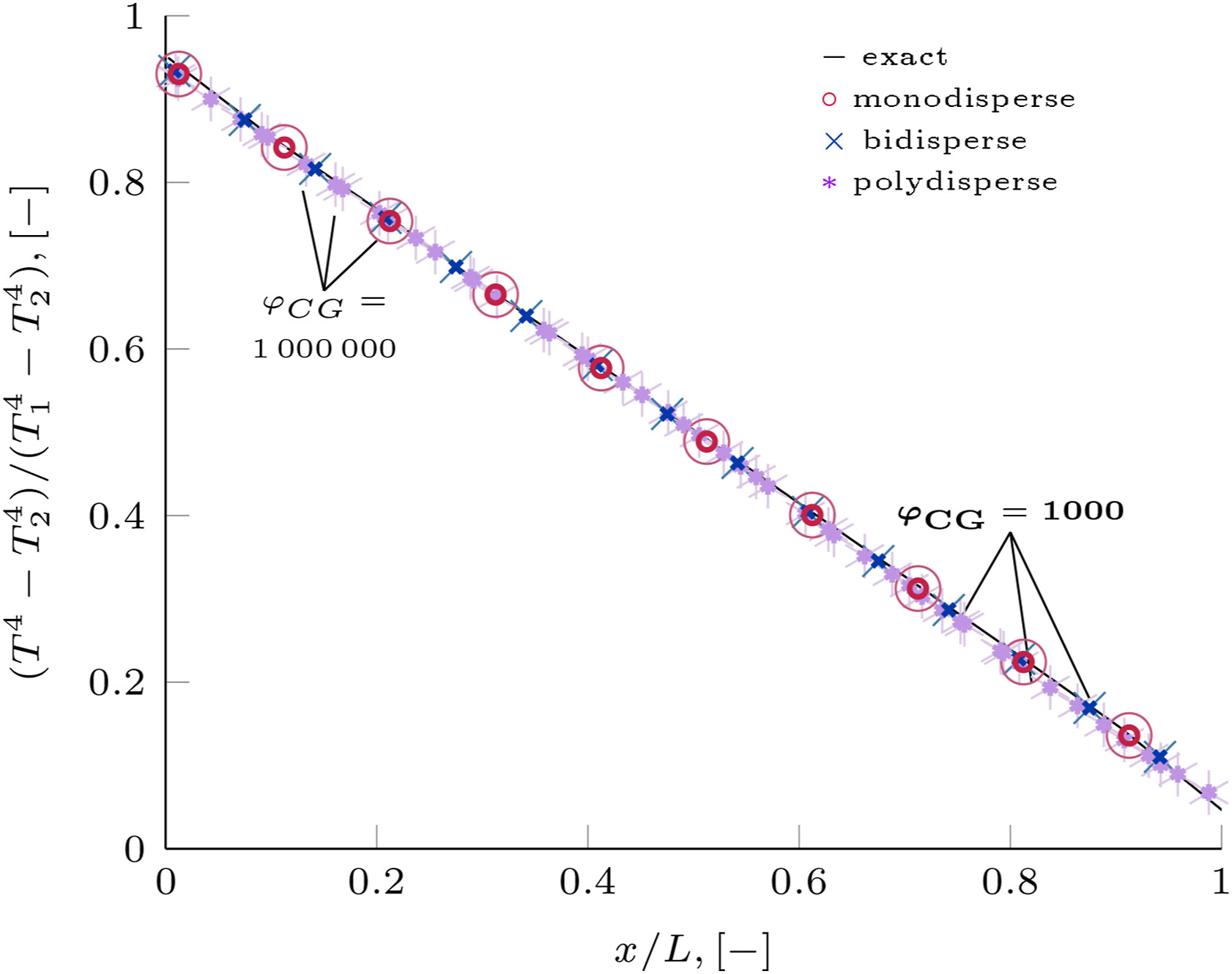
图3. τL=10时粗粒化对x轴向上辐射强度的影响
下图是τL=10时在双分散体系下采用平滑辐射扩散率及添加伪散射项分别修正P1模型计算出的全场平均热通量和温度的相对误差随网格数目的变化趋势并与未修正的计算结果对比,结果表明当单位长度上网格的数目达到50时,采用平滑辐射扩散率的方法基本能够完全消除热通量的极端振荡,相比之下采用添加伪散射项方法的效果较差,但是在计算域较小且颗粒数目较少时,添加伪散射项的方法较为有效,因为较大的平滑尺度可能会导致边界温度异常,对于温度的求解两种修正方法都展现出了较高的准确性(相对误差都小于10%)。
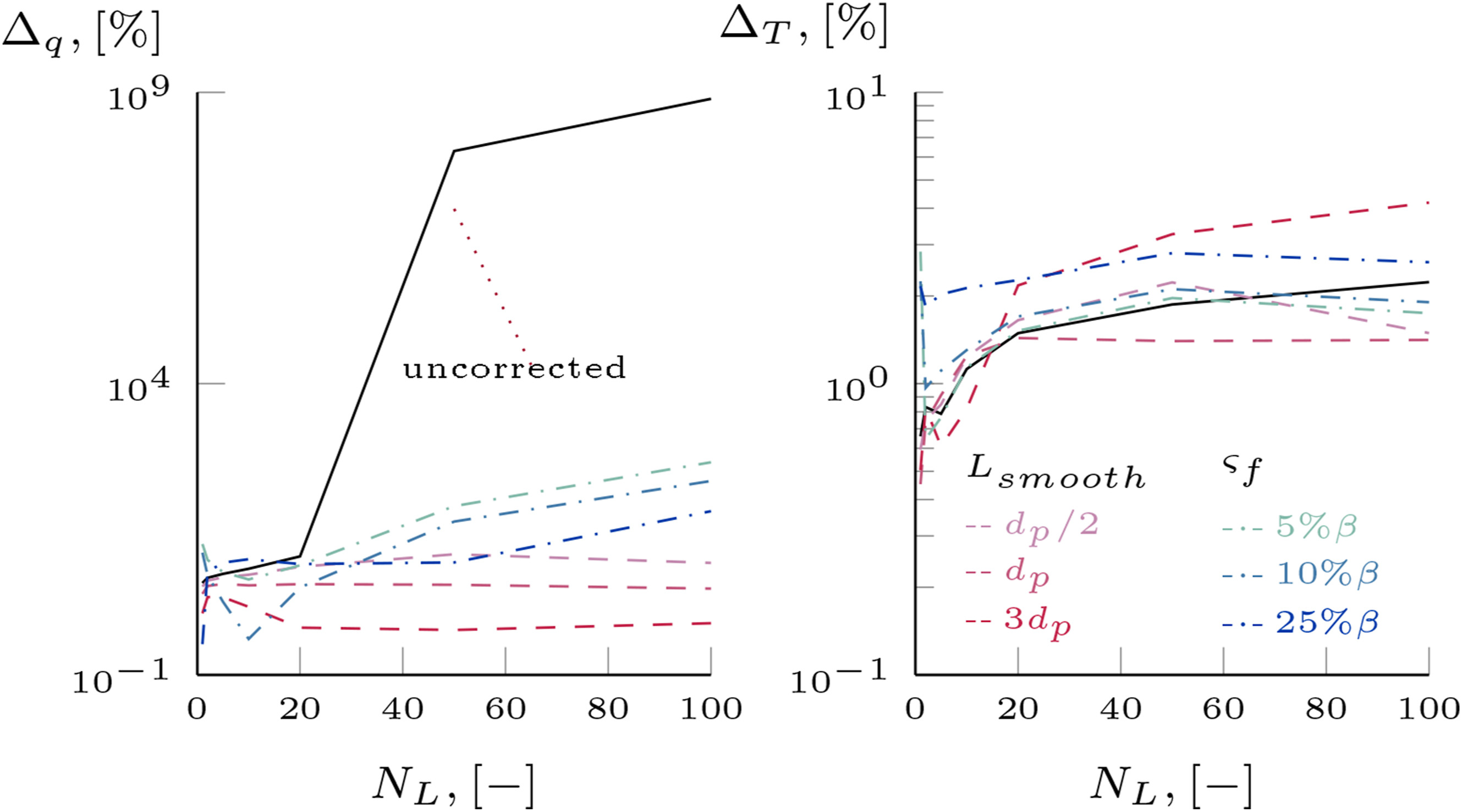
图4. 单位长度上不同的网格数目下τL=10时双分散体系中平均热通量和温度的相对误差变化情况
但从图5来看,即使采用平滑辐射扩散率或者添加伪散射项的方法消除了热通量振荡,局部热通量仍存在偏差。
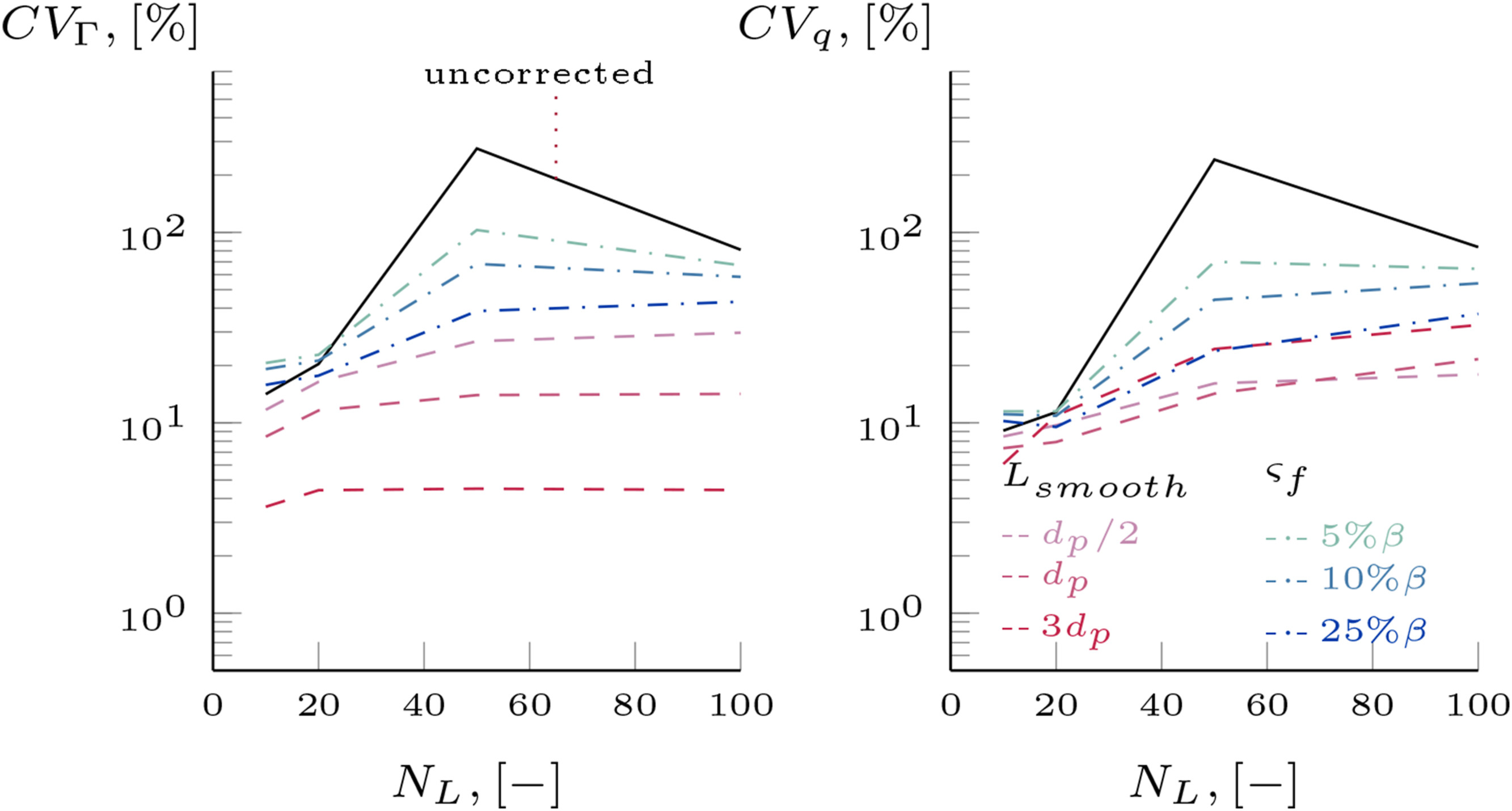
图5. 辐射扩散率与热通量的标准差和平均值的比值随网格数目变化的情况
结论
1.采用平滑辐射扩散率和添加伪散射项的方法都能减轻热通量的振荡,且平滑辐射扩散率基本上优于添加伪散射项,添加伪散射项更加适用于计算域较小且颗粒数目小于1000的情况。
2.即使采用平滑辐射扩散率或者添加伪散射项的方法消除了热通量振荡,局部热通量的偏差依旧存在,因此P1模型不太适合研究整个计算域的热通量变化。
3.P1模型对稳态和瞬态求解、单分散,双分散和多分散等不同体系及粗粒化都具有较好的适用性。
作者简介

Jelena Mačak, Doctoral Candidate, Graz University of Technology.
Jelena is a doctoral candidate in chemical and process engineering at Graz University of Technology. She holds a master’s degree in aeronautical engineering from Faculty of Mechanical Engineering and Naval Architecture in Zagreb, Croatia. From 2019 to 2022, she was a research assistant at DCS Computing GmbH. Her primary research interest is numerical modeling of heat transfer phenomena in particle-fluid systems.

Christoph Goniva, Co-founder, DCS Computing GmbH.
Christoph holds a PhD in mechatronics from Johannes Kepler University in Austria. He is the co-founder and managing partner of DCS Computing GmbH (since 2011), and of CFDEM research GmbH (since 2015). Prior to that, he worked as a scientist at the Christian Doppler Laboratory on particulate flow modelling. He currently focuses on modelling fluid-granular systems by means of CFD-DEM and DEM.

Stefan Radl, Associate Professor, Graz University of Technology.
Stefan holds a PhD in chemical engineering from Graz University of Technology (TU Graz), and was promoted with highest distinction in 2011. Since August 1st 2018, Stefan is an Associate Professor at TU Graz, where he holds a venia docendi for the subject “particle technology”. Prior to that, Stefan was a Post Doc at Princeton University (Dept. of Chemical and Biological Engineering, supervisor: Prof. Sankaran Sundaresan, 2011 to 2012), and an Assistant Professor at TU Graz (from 2012 to 2018). His current research focusses on computer simulation of gas-particle flows, associated calibration workflows and data management.
学术审核:西安交通大学周强教授
编辑:《颗粒学报》编辑部
文章信息
Mačak, J., Goniva, C., & Radl, S. (2023). Predictions of the P1 approximation for radiative heat transfer in heterogeneous granular media. Particuology, 82, 25-47. https://doi.org/10.1016/j.partic.2023.01.003.
