Modelling of heat transfer in moving granular assemblies with a focus on radiation using the discrete ordinate method: A DEM-CFD approach (Open Access)--颗粒学报PARTICUOLOGY

Modelling of heat transfer in moving granular assemblies with a focus on radiation using the discrete ordinate method: A DEM-CFD approach (Open Access)

Rezvan Abdi^*, Bo Jaeger, Enric Illana, Siegmar Wirtz, Martin Schiemann, Viktor Scherer

Institute of Energy Plant Technology, Ruhr-University Bochum, Universitätsstraße 150, 44780, Bochum, Germany

10.1016/j.partic.2025.02.024

Volume 100, May 2025, Pages 78-94

Received 18 November 2024, Revised 7 February 2025, Accepted 25 February 2025, Available online 14 March 2025, Version of Record 22 March 2025.

E-mail: Abdi@leat.ruhr-uni-bochum.de

Highlights

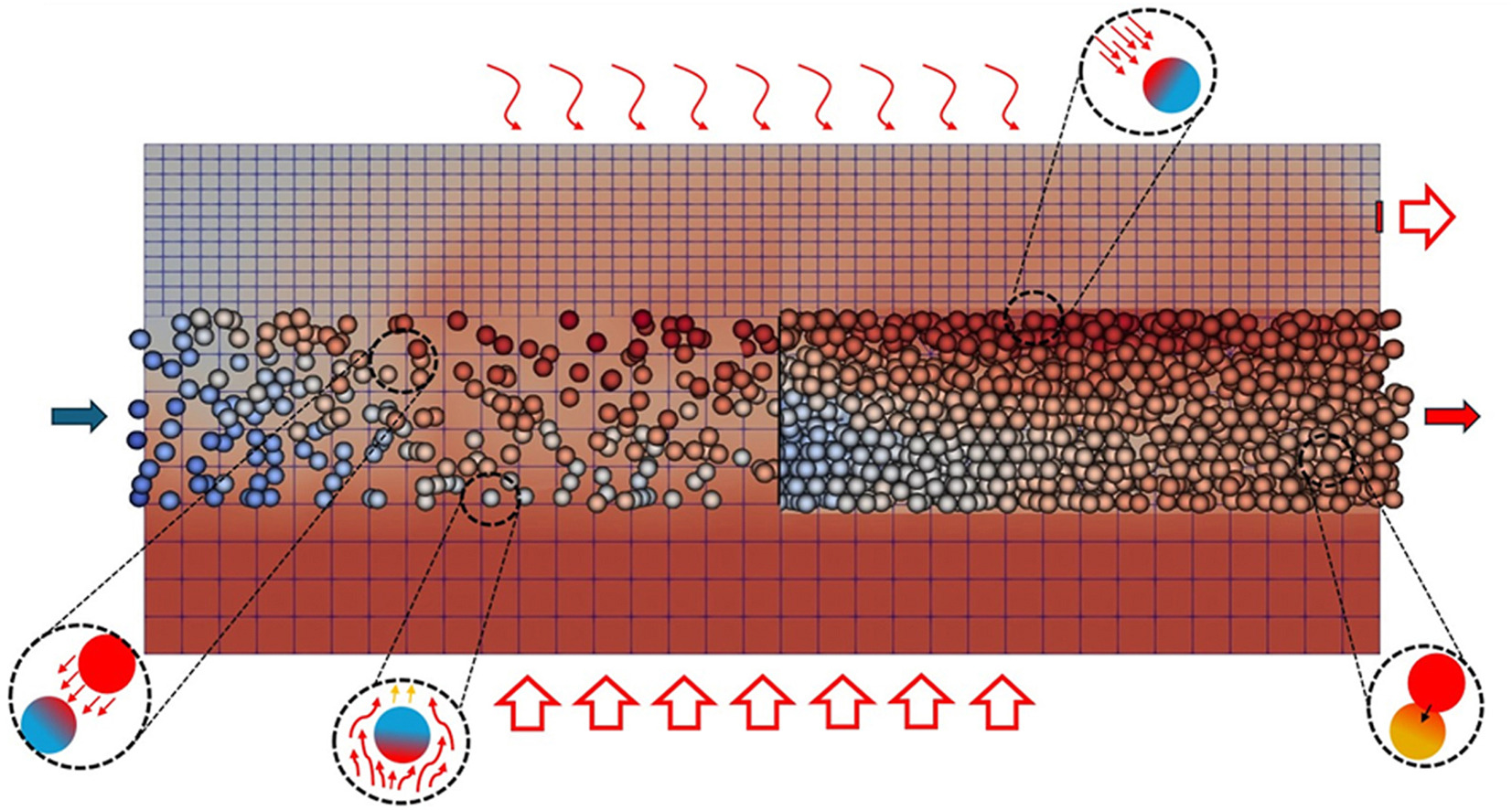
• Discrete Ordinates Method in DEM-CFD to simulate radiation in moving packed beds.

• Analysis of the influence of packing density on radiation penetration depth.

• Interplay of convective, solid-conduction and radiative heat transfer in packed beds.

• Conduction leads to a diffusive effect on temperature distribution in packed beds.

Abstract

Discrete Ordinates Method (DOM) is a model for thermal radiation exchange in opaque media. In this study, the DOM formulation is employed within the framework of the Discrete Element Method coupled with Computational Fluid Dynamics (DEM-CFD), thus including full radiative heat exchange among the phases involved. This is done by adjusting the absorption coefficient, emission coefficient, and net radiative heat flux of particles by incorporating local porosity into equations. A key objective is to represent radiation propagation for different packing densities in packed beds accurately.

The model is validated by comparing the results with available data from the literature for simulations with a P1 radiation model and corresponding experiments. The validation configuration is a heated box filled with spherical particles under vacuum conditions.

As an application example, the radiative heat exchange between an enclosure at high temperature and moving layers of spherical particles concurrently passed by a gas in crossflow is studied. Three packing densities (dilute, moderate, and dense) are examined to evaluate radiation penetration into the particle ensemble. Convective and contact heat transfer are also considered. The DEM-CFD coupling is a non-resolved approach, where the influence of particles on the flow field is accounted for by momentum and energy source terms together with a porosity field (Averaged Volume Method (AVM)).

Effect of convective, conductive and radiative heat transfer is analysed based on the evolution of incident radiation flux, spatial distributions of particle surface and fluid temperatures, and particle temperature histograms. It becomes obvious that radiation dominates the system, and that packing density defines the penetration depth of radiation. Conduction mainly leads to a smoothening of particle temperature distribution in the system.

Graphical abstract

Keywords

AVM; DOM radiation; DEM-CFD; OpenFOAM

文章导读