En
期刊文章
文章精选
当期目录
过刊浏览
高被引
高下载
特邀文章
专刊合集
待刊文章
Volume 102
您当前的位置：首页 > 期刊文章 > 当期目录 > Volume 102
Strength and friction dependency of the stress Lode angle in true triaxial configurations: A discrete element perspective
Shiva Prashanth Kumar Kodicherla a *, Minyi Zhu b *
a Department of Civil, Mining and Process Engineering, Namibia University of Science and Technology, Windhoek, Namibia b Department of Geotechnical Engineering, College of Civil Engineering, Tongji University, Shanghai, China
10.1016/j.partic.2025.04.009
Volume 102, July 2025, Pages 70-77
Received 24 February 2025, Revised 27 March 2025, Accepted 10 April 2025, Available online 18 April 2025, Version of Record 24 April 2025.
E-mail: prashanthetc1024@gmail.com; skodicherla@nust.na; 835192801@qq.com
Highlights

• Macroscopic response of granular material is affected by mean effective stress and intermediate stress ratio.

• Principal deviatoric stress stays stable with shear strain and rises with higher intermediate stress ratios.

• Principal deviatoric strain deviates from its initial value as shear strain increases.

• Peak state friction angle significantly affects peak stress ratio at Lode angle +30° compared to Lode angle −30°.


Abstract

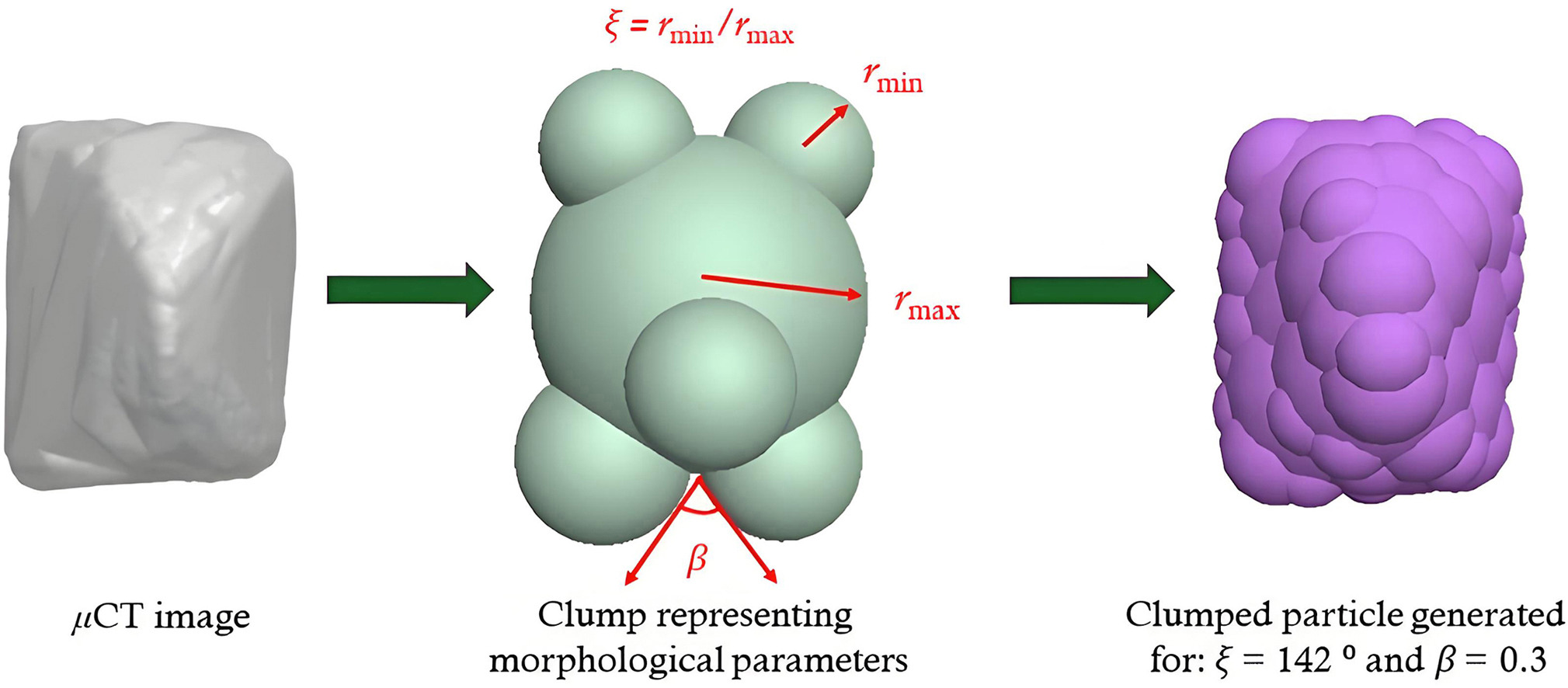
This article investigates the strength and frictional dependence on the stress Lode angle in drained true triaxial configurations using the discrete element method (DEM). A clump logic based on the multi-sphere (MS) approach within the commercial DEM software, particle flow code (PFC3D), was employed to simulate realistic particle shapes. The simulation results indicate that deviatoric stress initially exhibits strain hardening, followed by softening, while pure dilation occurs from the onset of shear. The evolutions of deviatoric stress and volumetric strains are found to be independent of both mean effective stress and intermediate stress ratios (b). The mobilized peak friction angle initially increases up to a certain value of b, then decreases with a further increase in b. The mechanical coordination number (MCN) and sliding contact fractions (SCF) remain unique and independent of b values. Moreover, the critical state friction angle has a significant influence on the stress ratios at the stress Lode angle θ = +30° when compared to θ = –30°.


Graphical abstract
Keywords
Clumped granular particles; Discrete element method; Intermediate stress ratio; True triaxial test
文章导读