En
期刊文章
文章精选
当期目录
过刊浏览
高被引
高下载
特邀文章
专刊合集
待刊文章
Volume 107
您当前的位置：首页 > 期刊文章 > 当期目录 > Volume 107
An improved particle neighbor search algorithm with multi-level cache optimization strategy for discrete element method using GPU
Hongze Li a b, Chun Feng c 1 *, Jili Feng a b 2 *
a State Key Laboratory for Tunnel Engineering, China University of Mining and Technology Beijing, 100083, Beijing, China
b School of Mechanics and Civil Engineering, China University of Mining and Technology Beijing, 100083, Beijing, China
c Institute of Mechanics, Chinese Academy of Sciences, No 15 Beisihuanxi Road, Haidian District, 100190, Beijing, China
10.1016/j.partic.2025.09.013
Volume 107, December 2025, Pages 1-10
Received 31 July 2025, Revised 12 September 2025, Accepted 22 September 2025, Available online 26 September 2025, Version of Record 3 October 2025.
E-mail: fengchun@imech.ac.cn; fjl@cumtb.edu.cn
Highlights

• The provided algorithm combines CLL method with Morton encoding as well as idea of VT method.

• The provided algorithm forms a multi-level cache optimization strategy.

• The computational efficiency of the algorithm is significantly enhanced.


Abstract

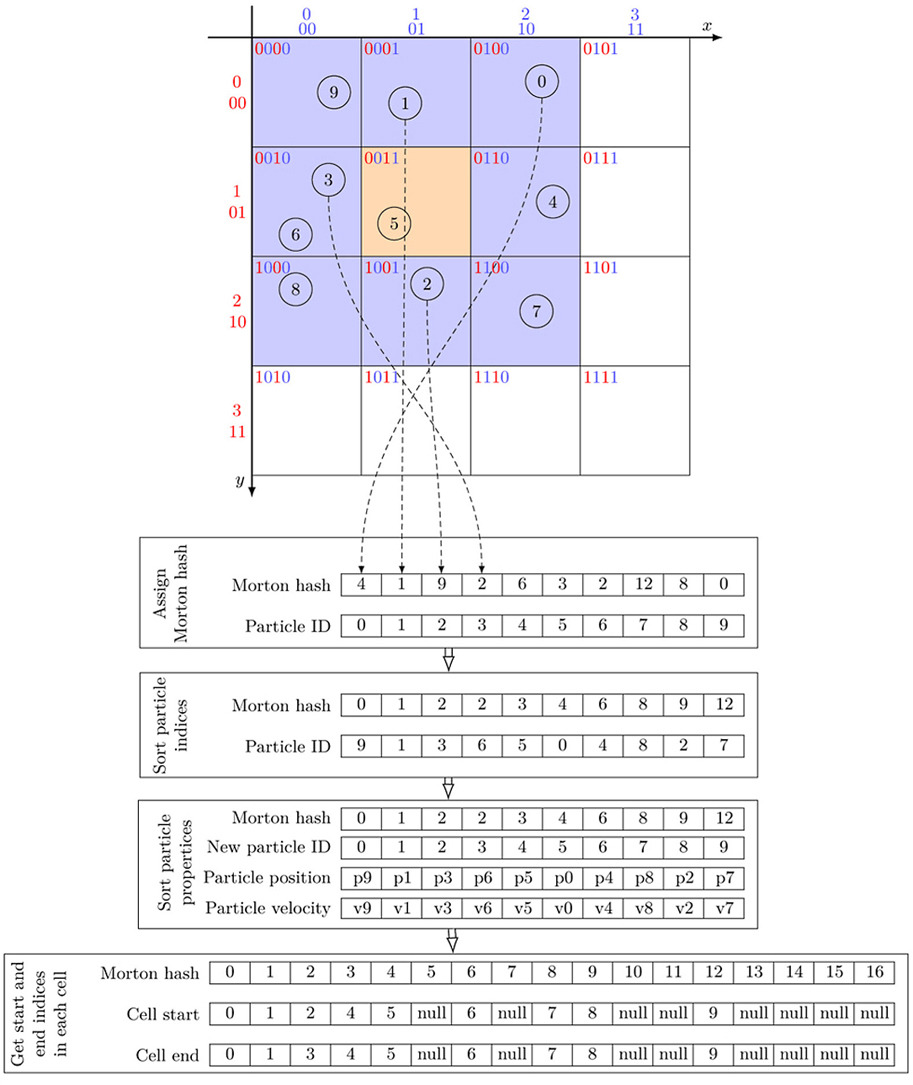
This paper proposes an improved particle neighbor search algorithm, focusing on optimizing computational efficiency and memory usage in large-scale particle system simulations. By partitioning the simulation space into grids and combining it with Morton encoding, it ensures that adjacent grids are stored contiguously in memory, thereby enhancing the locality of data access and reducing the probability of cache misses. In the particle sorting phase, Morton encoding is used to rearrange the particles, further enhancing memory continuity and leveraging the hardware cache's prefetching mechanism to reduce data read latency. The algorithm also incorporates the idea of the Verlet table method by setting a sorting threshold to optimize the sorting process, avoiding redundant calculations and unnecessary sorting operations. Through the above optimization methods, a multi-level cache optimization strategy is achieved, significantly improving the algorithm's performance and memory utilization efficiency. Experimental results show that the algorithm proposed in this paper has significant advantages in large-scale particle simulations.

Graphical abstract
Keywords
Neighbor search; Discrete element method; Morton encoding; Cell linked list method; Verlet table method
文章导读